IL CAMPO TRAPEZOIDALE
Antonio ha un campo a forma di trapezio. I suoi quattro lati misurano un numero intero di metri e la sua area è espressa da un numero intero di metri quadrati. Inoltre, sappiamo che la base maggiore misura 70 m e che i due lati obliqui misurano rispettivamente 104 e 50 metri. Quanto misura, in metri, la base minore del campo di Antonio?
26
punti
Livello 0
Nota: il risultato, ovvero la base minore, è 4 m
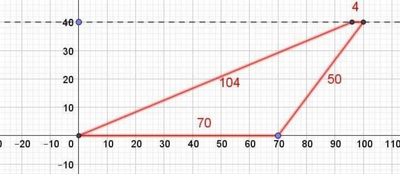
Secondo me c'è qualcosa da rivedere nei dati.
Se si chiamano a e c le proiezioni dei lati obliqui sulla base maggiore
a + b + c = 70 => a + c < 70
Per il Teorema di Pitagora sui due triangoli rettangoli laterali
che hanno per ipotenusa ciascuno dei lati obliqui
{ a^2 + h^2 = 104^2
{ c^2 + h^2 = 50^2
sottraendo a^2 - c^2 = 10816 - 2500 = 8316
(a - c) ( a + c ) = 8316
Uno di questi fattori, il maggiore, deve essere maggiore della radice quadrata di 8316,
che è più di 91. Quindi
a + c > 91
impossibile se a + c < 70.
Sbaglio io, oppure la traccia ?
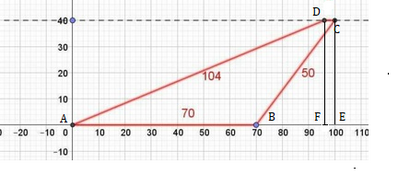
------------------ Aggiornamento, dopo aver visto la figura
per il teorema di Pitagora puoi scrivere
( d è la distanza fra estremo destro della base maggiore e proiezione dell'estremo destro
della minore sulla maggiore e b è la lunghezza della base minore )
d^2 + h^2 = 50^2
(70 + d - b)^2 = 104^2
Sottraendo
(70 + d - b)^2 - d^2 = 104^2 - 50^2
scomponendo
(70 + d - b + d)(70 + d - b - d) = 10816 - 2500
(70 + 2d - b) (70 - b) = 8316
M*m = 8316
M e m sono due divisori di 8316
e dovendo risultare
70 + 2d - b = M
70 - b = m
per differenza 2d = M - m => d = (M - m)/2
e b = 70 - m
m e M possono essere
(1,8316)
(2,4158)
(3,2772)
(4,2079)
(6,1386)
(7,1188)
(9, 924)
(11,756)
(12,693)
(14,594)
(18, 462)
(21, 396)
(22,378)
(27,308)
(28,297)
(33,252)
(42,198)
(44,189)
(54,154)
(63, 132)
(66,126)
(77,108)
(84,99)
Sono molti e spero di non averne dimenticato nessuno.
Tuttavia, poichè deve essere h^2 = 50^2 - d^2
d non può superare 50
(M - m)/2 <= 50
M - m <= 100
e quindi solo le ultime 5 coppie andrebbero bene. I valori di d che ne risulterebbero
sono
(54, 154) d = 50 no perchè sarebbe h = 0
(63, 132) d = 34.5 no perchè avremmo problemi con l'area
(66, 126) d = 30
(77, 108) d = 16.5 no perchè avremmo problemi con l'area
(84, 99) d = 7.5 no perchè avremmo problemi con l'area
allora d = 30 => m = 66 e b = 70 - m = 70 - 66 = 4
47919
punti
Livello 7
@eidosm ho notato anch’io che il trapezio con i dati conosciuti non è costruibile. Il quesito è però così’ formulato anche nel testo originale. Si tratta di un esercizio facente parte del gruppo di esercizi pubblicati come prova di allenamento per i giochi matematici che ci saranno in questi giorni organizzati dalla Bocconi
Un'ipotesi è che voglia testare questo tipo di competenza, il riconoscimento di un'impossibilità. Oppure aveve pensato a qualche dato numerico errato.
@eidosm i dati del problema sono corretti e il trapezio è costruibile...ho postato una foto.
@MatteoG hai ragione non avevo preso in considerazione l’ipotesi del trapezio ottusangolo...
Se si sta attenti si può osservare che si possono usare due terne pitagoriche, in questo modo si può ricavare la base minore. Terne pitagoriche: (50,40,30) e (104,96,40)
45
punti
Livello 0
@montalbano giusto. Trattandosi di quesito espresso nei giochi matematici e’ stato sicuramente pensato per utilizzare le terne pitagoriche
vista la figura , l'approccio più semplice consiste nel considerare 50 come parte di una terna pitagorica il che da due possibili altezze EC (30 o 40)
104^2-30^2 non è un quadrato e , quindi, AF non può essere un intero
104^2-40^2 lo è (8√13^2-5^2 = 8*12 = 96
CD =AE-AF = (70+30)-96 = 4
114464
punti
Genius II
