[Risolto] problema di geometria analitica

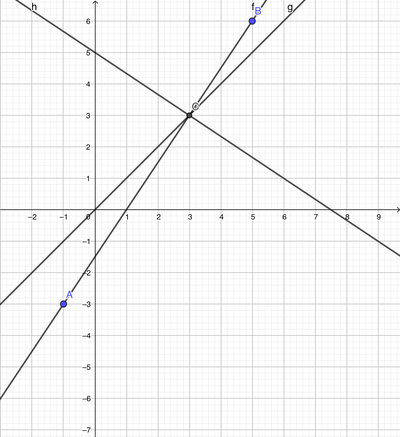
1. Retta AB passante per i punti A(-1,-3) e B (5,6)

Applichiamo la formula passante per due punti

(y-yA)/(yB-yA) = (x-xA)/(xB-xA)

(y+3)/(6+3) = (x+1)/(5+1)

3x-2y-3 = 0

2. Punto P(x,y) appartenente alla retta 3x-2y-3 = 0.

Il punto P è caratterizzato dal fatto che y=x.

Risolviamo il sistema formato della due equazioni.

{y = x

{3x-2y-3 = 0

per sostituzione. 3x-2x-3=0 cioè x=3 & y=3

La coordinate di P sono P(3,3)

3. retta perpendicolare alla retta AB passante per P(3,3)

• coefficiente angolare retta AB. m = 3/2
• coefficiente angolare perpendicolari alla retta AB m'=-2/3.
• equazione retta passante per il punto P

y-yP = m'(x-xP)

y-3 = (-2/3)(x-3)

2x+3y-15 = 0

Retta AB: y=mx+q

Sostituiamo all'interno di questa equazione le coordinate di A e B:

-3=-m+q

6=5m+q

Dobbiamo risolvere il sistema sopra; moltiplichiamo la prima equazione per -1 e sommiamo in colonna:

3=m-q

6=5m+q

-------------

9=6m

m=9/6=3/2

q=m-3=3/2-3=-3/2

Retta AB: y=3/2 x-3/2

Implicitiamola; moltiplichiamo tutto per 2:

2y=3x-3

Portiamo tutti i termini a sinistra e cambiamo i segni:

retta AB: 3x-2y-3=0

P appartenente ad AB tacle che P(x;x):

3x-2x-3=0

x-3=0

x=3

y=x=3

P(3;3)

r perpendicolare ad AB; il coefficiente di r sarà -2/3, cioè l'antireciproco di 3/2 (coefficiente di AB):

r: y=-2/3 x+q

P è un punto di r, allora sostituiamo le sue coordinate all'interno dell'equazione sopra:

3=-2/3 * 3+q

3=-2+q

q=5

r: y=-2/3 x+5

Moltiplichiamo per 3:

3y=-2x+15

Portiamo tutti i termini a sinistra:

r: 2x+3y-15=0

@bubbazzo.

Ciao.

retta AB  con A(-1,-3) e B( 5,6)

(y+3)/(x+1)=(6+3)/(5+1)  ————>y+3=3/2*(x+1)

quindi 2y+6=3x+3—————>3x-2y-3=0

punto P

{3x-2y-3=0

{y=x

per sostituzione3x-2x-3=0—->x=3;y=3  quindi. P(3,3)

retta perpendicolare a AB per P: m= -2/3 ( AB ha m=3/2)

y=-2/3*x+q  ———> 3=-2/3*3+q quindi

3=-2+q   Quindi q=5

equazione y= -2/3*x+5 anche 2x+3y-15=0

La retta congiungente due dati punti A(a, p) e B(b, q) è
* per a = b: AB ≡ x = a
* per p = q: AB ≡ y = p
* per (p = k*a) & (q = k*b): AB ≡ y = k*x
* per a != b: AB ≡ y = ((p - q)/(a - b))*x + (a*q - b*p)/(a - b)
IN QUEST'ESERCIZIO
Con
* A(- 1, - 3), B(5, 6)
si ha
* AB ≡ y = ((- 3 - 6)/(- 1 - 5))*x + (- 1*6 - 5*(- 3))/(- 1 - 5) ≡
≡ y = (3/2)*(x - 1)
con pendenza m = 3/2 e punto cursore P(x, (3/2)*(x - 1)).
Il fascio delle sue perpendicolari, di pendenza m' = - 2/3, è
* p(q) ≡ y = q - (2/3)*x
------------------------------
Ogni punto P di ascissa uguale all'ordinata ha coordinate P(x, x).
Per appartenere ad AB deve avere
* x = (3/2)*(x - 1) ≡ x = 3 = y
La retta p(q) per P(3, 3) deve soddisfare al vincolo
* 3 = q - (2/3)*3 ≡ q = 5
quindi è
* p(5) ≡ y = 5 - (2/3)*x