Buongiorno a tutti, potreste aiutarmi a risolvere il punto B di questo problema?
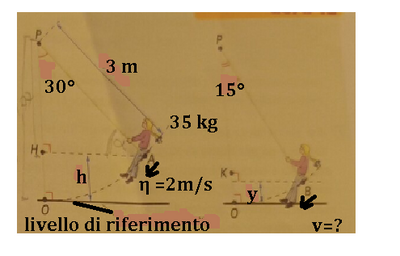
Un'altalena, che con un bambino seduto ha una massa di 35 kg, è costruita con una fune lunga 3,0 m. Quando viene lasciata oscillare, con una velocità iniziale di 2,0 m/s, l'angolo formato con la verticale è 30 gradi. Trascurando gli attriti, calcola:
a) la velocità dell'altalena e la sua energia cinetica iniziale quando scendendo, forma un angolo di 15° rispetto alla verticale
B ) La velocità massima che può raggiungere l'altalena
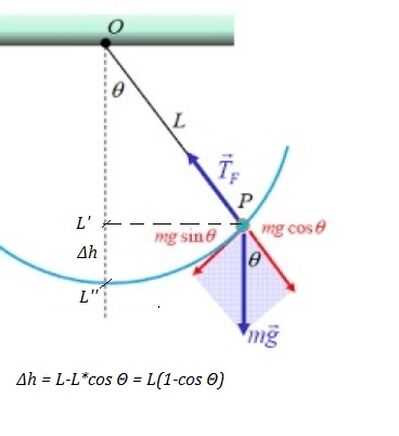
Allego il problema simile, per avere un'idea del disegno, e il problema da risolvere. Il punto a l'ho fatto, vorrei solo capire come risolvere il punto B.
Grazie a tutti coloro che risponderanno