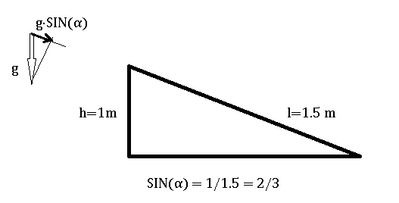
Supponiamo di trovarci su un pianeta sconosciuto e di voler misurare l'accelerazione di gravità. Abbiamo a disposizione un piano inclinato alto 1 m e lungo 1,5 m, una massa e un cronometro. Misuriamo il tempo affinché la massa cada, partendo da ferma, dalla cima del piano inclinato fino alla base. Otteniamo un valore di 1,4 s. Indica l'accelerazione di gravità sul pianeta.
73
punti
Livello 0
Sia g l'accelerazione di gravità del pianeta.
La massa si muove lungo il piano inclinato per effetto della componente di gravità lungo il piano stesso : g·SIN(α) essendo SIN(α) = 1/1.5= 2/3
In assenza di attriti, la legge oraria della massa m lungo il piano inclinato di scriverà:
x = 1/2·(2/3·g)·t^2-----> x = g·t^2/3
da cui: g = 3·x/t^2
Per: x = l = 1.5 m; t = 1.4 s si ottiene:
g = 3·1.5/1.4^2----> g = 2.296 m/s^2 circa
94774
punti
Genius II
@lucianop 👍👌👍
2L = g*h/L*t^2
g = 2L^2/(h*t^2) = 2*2,25/(1*1,96) = 2,30 m/s^2
114462
punti
Genius II
* 1,4 s = 7/5 s
* tg(θ) = (1 m)/(1.5 m) = 2/3 (2^2 + 3^2 = 13)
* sin(θ) = sin(arctg(2/3)) = 2/√13
* cos(θ) = cos(arctg(2/3)) = 3/√13
* a = g*sin(θ) ≡ g = a/sin(θ) = a*√13/2
Dalla legge oraria
* y(t) = h - (a/2)*t^2
si ha il tempo di volo T > 0 risolvendo
* (0 = h - (a/2)*T^2) & (T > 0) ≡ T = √(2*h/a)
e infine, mettendo tutto insieme,
* (g = a*√13/2) & (h = 1) & (√(2*h/a) = 7/5) ≡
≡ (a = 50/49) & (g = 25*√13/49 ~= 1.839566977 ~= 1.84) m/s^2
57382
punti
Genius I
@exprof ...mi sa che eri partito per la tangente 🤭....meglio partire per le vacanze, e che le tue sian serene
