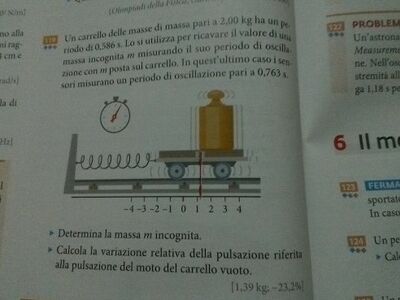
Un carrello delle masse di massa pari a 2,00 kg ha un periodo di 0,586 s. Lo si utilizza per ricavare il valore di una massa m misurando il suo periodo di oscillazione con m posta sul carrello. In quest'ultimo caso i sensori misurano un periodo di oscillazione pari a 0,763 s.
Determina la massa m incognita (1,39 kg)
Calcola la variazione relativa alla pulsazione riferita alla pulsazione del moto del carrello vuoto (-23,2%)
Grazie.