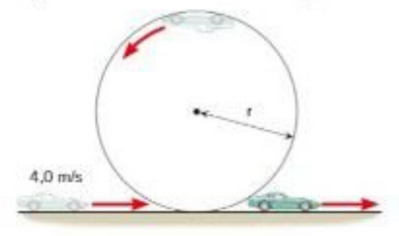
La figura rappresenta una versione del cosiddetto “giro della morte” compiuto da una piccola automobile su una pista a forma di anello.
> Se la velocità iniziale dell'automobile é 4,0m/s, qual é il valore massimo del raggio r dell'anello perché l'automobile resti sempre a contatto con la pista? [0,327 m]
Pensavo bastasse considerare il momento in cui l'automobile si trova nel punto più alto della pista e quindi eguagliare la forza peso alla forza centripeta, da lì semplificare la massa e calcolare quindi il raggio come v^2/g, ma il risultato non coincide.
Quale sarebbe il corretto procedimento?