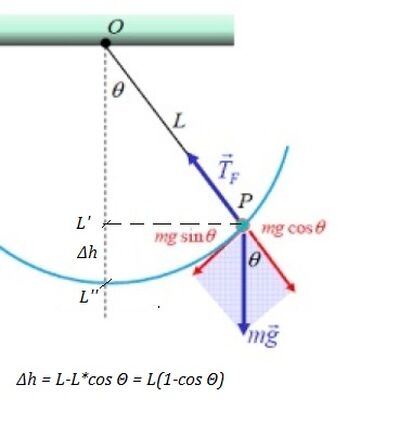
Una massa $M=1 \mathrm{~kg}$ è poggiata su un piano orizzontale scabro tale che il coefficiente di attrito statico tra corpo $\mathrm{M}$ e piano è $\mu=0.5$. Come riportato in figura, un cavo ideale passa attorno alla carrucola ideale $\mathrm{C}$ e collega la massa $\mathrm{M}$ a un'altra massa $\mathrm{m}=0.3 \mathrm{~kg}$, sospesa nel vuoto. Determinare il massimo valore dell'ampiezza di oscillazione della massa $\mathrm{m}$ compatibile con la condizione che la massa $\mathrm{M}$ permanga in equilibrio statico. [Suggerimento: considerare che in un pendolo semplice, detta $\theta_0$ l'ampiezza dell'oscillazione, la tensione del cavo a cui è collegata una massa $\tilde{m}$ del pendolo in funzione dell'angolo $\theta$ formato con la verticale è data dalla relazione $\mathrm{T}(\theta)=\widetilde{m} g\left(3 \cos \theta-2 \cos \theta_0\right)$.]