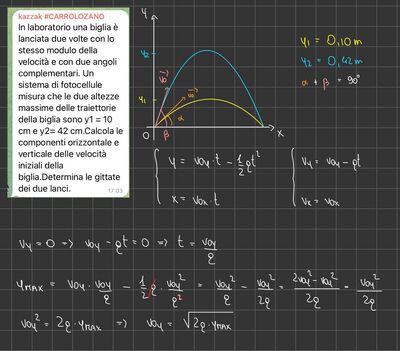
In laboratorio una biglia è lanciata due volte con lo stesso modulo della velocità e con due angoli complementari. Un sistema di fotocellule misura che le due altezze massime delle traiettorie della biglia sono $y_{1}=10 \mathrm{~cm}$ e $y_{2}=42 \mathrm{~cm}$
Calcola le componenti orizzontale e verticale delle velocità iniziali della biglia.
Determina le gittate dei due lanci.
Suggerimento: ricorda che $\sin \left(90^{\circ}-\alpha\right)=\cos a$ e $\cos \left(90^{\circ}-\alpha\right)=\sin \alpha$
$$
[2,9 \mathrm{~m} / \mathrm{s} ; 1,4 \mathrm{~m} / \mathrm{s} ; 83 \mathrm{~cm}]
$$