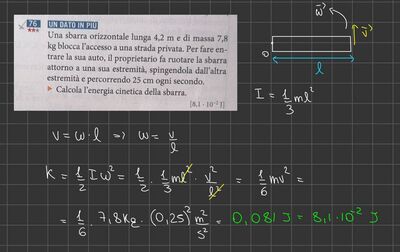
Una sbarra orizzontale lunga 4,2m e di massa 7,8kg blocca l'accesso a una strada privata. Per far entrare la sua auto, il proprietario fa ruotare la sbarra attorno a una sua estremità, spingendola dall'altra estremità e percorrendo 25cm ogni secondo. Calcola l'energia cinetica (K) della sbarra.
risultato [8,1*10^-2 J]