problema di fisica

Nella figura sotto è ripotato il grafico della accelerazione della palla da bowling , il grafico della velocità ed il grafico dello spostamento. Il problema posto richiede:

a) la velocità Max della palla

b) spazio percorso quando a=0 ( accelerazione nulla)

Le due domande sono interconnesse.

a=dv/dt= v’

vmax si ha per v’=0  cioè per a=0

Quindi:

a=0 per t=30/12=2.5 s

essendo V= 30t-6t^2 per t =2.5 s si ha:

vmax=37.5 m/s

Integrando ulteriormente la velocità si ottiene lo spazio percorso:

s= 15t^2-2t^3 per t=2.5 s

s=62.5 m

L'esercizio é estremamente semplice, ma rinuncio a svolgerlo senza gli integrali (immediati).

Parte a)

vo = 0 =>   v(t) = S (30 - 12 t) dt = 30 t - 6t^2   (m/s)

il profilo temporale é parabolico => il massimo é nel vertice

t* = -b/(2a) = -30/(-12) = 2.5 s

vmax = v(2.5) = (30*2.5 - 6*6.25) m/s = 37.5 m/s

Parte b)   Quando a = 0, t = t* = 2.5 s

per cui s(t) = S (30 t - 6 t^2) dt = ( 15 t^2 - 2t^3 + C ) m

in cui la costante C può essere posta uguale a zero

scegliendo l'origine del riferimento in modo opportuno.

In ogni caso  D = s(2.5) - s(0) =

= [ (15 * 6.25 - 2*2.5^3 + C) - C ] m = (93.75 - 31.25) m =

= 62.5 m.

a(t) = - 12 t + 30 m/s^2;

a = dv / dt; l'accelerazione è la derivata prima della velocità.

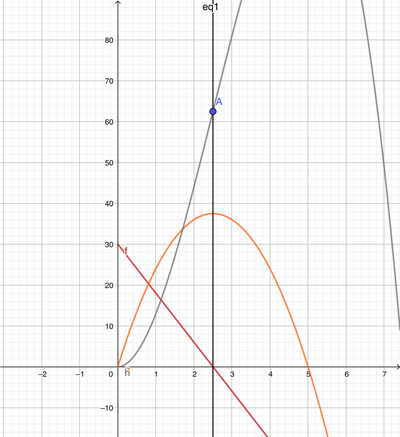
v max si ha   quando dv/dt = 0;  a(t) = 0;

- 12 t + 30 = 0; l'accelerazione diventa 0, troviamo il tempo t.

t = 30/12 = 2,5 s;  [al tempo t = 2,5 s,  abbiamo la velocità massima v max].

v = integrale da 0 a t di [- 12 x + 30] in dx;

v = [- 6x^2 + 30x] calcolato fra 0 e t ;

v(t) = - 6t^2 + 30 t;  

t = 2,5 s;

v max = - 6 * 2,5^2 + 30 * 2,5 = - 37,5 + 75 = + 37,5 m/s;

t = 2,5 s; accelerazione = 0 m/s^2;

S(t) è l'integrale della velocità:

St) = integrale da 0 s a 2,5 s di[- 6t^2 + 30 t] in dt;

S(t) = [- 6t^3 / 3 + 30t^2/2 ] da 0 a 2,5 s;

S(t) =  - 2 t^3 + 15 t^2;

S = - 2 * 2,5^3 + 15 * 2,5^2 = - 31,25 + 93,75;

S = 62,5 m. 

Ciao @_manuelreyes_

Un punto materiale, all'istante zero fermo nell'origine delle ascisse, è soggetto all'accelerazione
* a(t) = (30 - 12*t) m/s^2
quindi si muove con velocità
* v(t) = ∫ [u = 0, t] (30 - 12*u)*du = - 6*(t - 5)*t m/s
occupando le posizioni
* x(t) = ∫ [u = 0, t] (- 6*(u - 5)*u)*du = (15 - 2*t)*t^2 m
---------------
La velocità massima è al vertice della parabola
* v(t) = - 6*(t - 5)*t <= v(5/2) = 75/2 = 37.5 m/s = 135 km/h
---------------
L'accelerazione s'annulla, prima d'invertirsi, all'istante t = 5/2 quando la velocità è massima e la posizione è
* x(5/2) = (15 - 2*5/2)*(5/2)^2 = 125/2 = 62.5 m
che è anche la richiesta misura del cammino percorso.