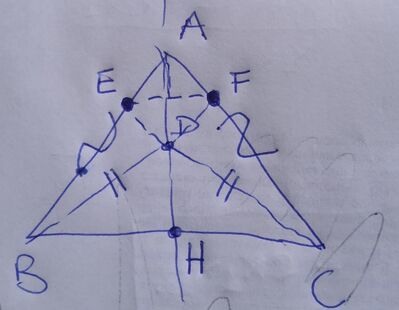
Sia ABC un triangolo isoscele sulla base BC. Un triangolo BDC, isosceles sulla base BC, ha il vertices D interno al triangolo ABC. Dimostra che: a. la semiretta AD è bisettrice dell’angolo BAC b. la semiretta AD è bisettrice dell’angolo BDC c. detti E e F due punti appartenenti rispettivamente ad AB e AC tali che BE congruente CF, il triangolo EDF è isoscele
3
punti
Livello 0
user1234
I triangoli ABC e DBC sono isosceli sulla base comune BC. AH e DH sono le altezze relative alla base. Sappiamo che l'altezza relativa alla base è anche mediana e bisettrice dell'angolo al vertice. La retta passante per i punti A, D, H è quindi bisettrice degli angoli al vertice.
I segmenti EC = BF poiché il triangolo è isoscele e BE = CF
I segmenti BD = CD poiché il triangolo BDC è isoscele.
ED = DF in quanto differenza di segmenti congruenti.
Il triangolo EDF è isoscele sulla base EF
76754
punti
Genius II
