buongiorno, qualcuno saprebbe cortesemente svolgere il seguente problema?
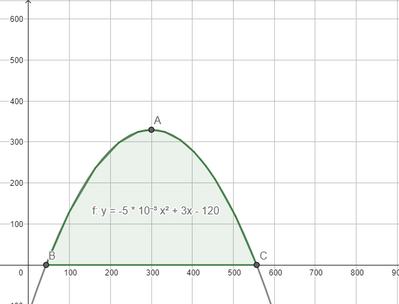
Una ditta produttrice di polvere insetticida sostiene un costo fisso giornaliero di € 120 e una spesa variabile di € 3,20 per ogni kilogram- mo di insetticida. La ditta prevede di ricavare dalla vendita € 6,20 al kilogrammo, con una spesa di vendita, in euro, pari allo 0,5% del qua- drato del numero di kilogrammi venduti. Quanto insetticida deve vendere giornalmente la ditta per avere il massimo guadagno? Quali sono i limiti di produzione per essere in attivo?
[300 kg al giorno; tra i 43 kg e i 557 kg]
grazie in anticipo a chiunque mi aiuterà 🙂