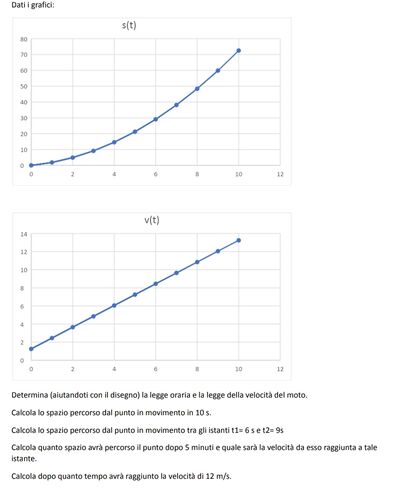
Qualcuno mi può aiutare con questo esercizio, non l'ho capito, se potete anche spiegarmi il perché di certi procedimenti ve ne sarei grato
Determina (aiutandoti con il disegno) la legge oraria e la legge della velocità del moto
Calcola lo spazio percorso dal punto in movimento in 10 s.
Calcola lo spazio percorso dal punto in movimento tra gli istanti t1= 6s e t2= 95
Calcola quanto spazio avrà percorso il punto dopo 5 minuti e quale sarà la velocità da esso raggiunta a tale
istante.
Calcola dopo quanto tempo avrà raggiunto la velocità di 12 m/s.