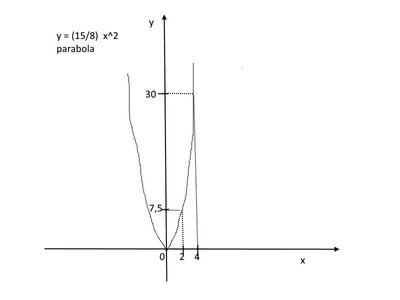
Un pentagono $A B C E D$ è formato dall'unione di un rettangolo $A B C D$ e di un triangolo isoscele $D C E$, di base $C D$. Il lato $A B$ è $\frac{3}{2}$ di $B C$, mentre l'altezza $E H$ relativa alla base $C D$ del triangolo $D C E$ è la metà di $B C$. Indicata con $x$ la misura di $B C$, determina la funzione che rappresenta l'area del pentagono in funzione di $x$. Traccia il grafico della funzione indipendentemente dalle limitazioni geometriche, mettendo in evidenza il tratto relativo al problema.
$$
\left[y=\frac{15}{8} x^2, \operatorname{con} x>0\right]
$$
Buongiorno qualcuno sa come si risolve questo problema? Grazie in anticipo