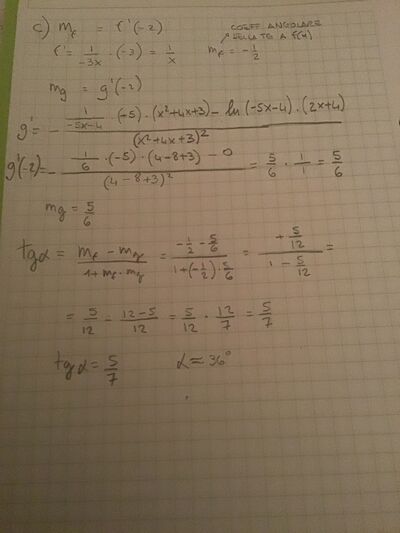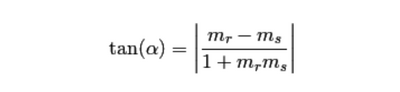Date le funzioni $f(x)=\ln (-3 x)$ e $g(x)=-\frac{\ln (-5 x-4)}{x^2+4 x+3}$
a. determina il loro dominio;
b. verifica che entrambi i grafici passano per il punto $P(-2 ; \ln 6)$;
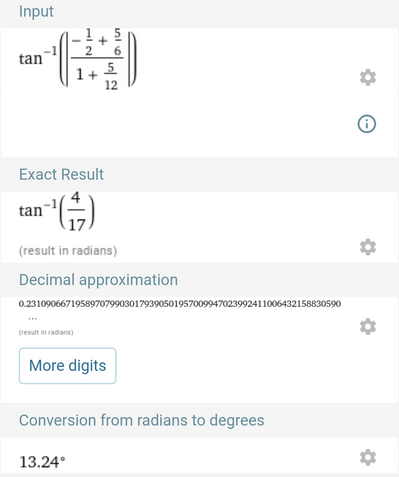
c. determina l'angolo acuto formato dalle tangenti ai grafici delle due curve in $P$, approssimandolo a gradi e primi sessagesimali;
d. studia la continuità di $g(x)$ in $x=-1$ e in $x=-3$.
[a) $D_f: x<0, D_{g^{\prime}}: x<-\frac{4}{5} \wedge x \neq-1 \wedge x \neq-3$; c) circa $\left.13^{\circ} 14^{\prime}\right]$
Ciao a tutti. Ho dei problemi a svolgere il punto c di questo problema, non so se sbaglio procedimento o ci sono errori di calcolo.
in pratica prima cerco il coefficiente angolare della retta tg alla f(x), per farlo calcolo la derivata di f(x) e poi sostituisco a x l’ascissa del punto.
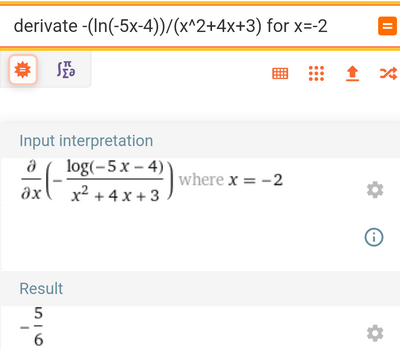
lo stesso faccio per trovare il coefficiente angolare della retta tg alla g(x)
poi se non sbaglio posso trovare la tg del mio angolo con la formula
= (m1-m2)/1+m1*m2
ma non mi viene…