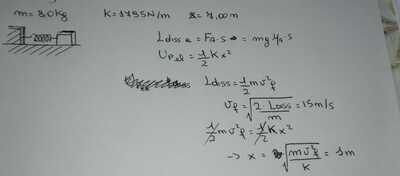Salve, un corpo di massa $8.0kg$ poggiato su una superficie orizzontale, legato ad una molla di costante elastica $K=1795N/m$. La molla, inizialmente è compressa di deltax. Il corpo percorre $x=7.0m$ prima di fermarsi.
Qual'è il valore della compressione iniziale se l'energia dissipata per attrito è $900J$
Uso sempre il teorema dell'energia.
$900= (1/2)*(1795)(49m)-(1/2)*(1795)*(x)$
$900=43977.5-987.5x^2$
$987.5x^2=43977.5-900$
$6.6m$
Credo sia sbagliato?
In cosa ho sbagliato? Grazie
824
punti
Livello 1
L'energia dissipata necessaria a fermare il corpo sarà pari all'energia potenziale elastica iniziale.
3817
punti
Livello 4
@anguus90 tra i possibili risultati:
$1.0014m$
$1.0028m$
$0.33380m$
$7.0809*10^-2$
$78.48m$
$42.426m$
@anguus90 sei sicuro? io credo che il corpo si fermi con la molla non in posizione di quiete, ma con dell'energia elastica ancora immagazzinata, tale che però la forza elastica non sia in grado di superare la forza di attrito statico. Però forse mi sto complicando la vita inutlmente
@anguus90 il risultato corretto qual'è? Tra quelli che ho messo?
secondo i miei calcoli 1,0014m, ho approssimato a 1 non pensando avessi le opzioni di risposta. @sebastiano ho capito cosa intendi, però anche quando la forza elastica non sarà più in grado di spostare il corpo, ammesso che probabilmente la molla non si fermerà in posizione di riposo, l'energia potenziale residua verrebbe dissipata sotto altre forme di energia, dunque nella conservazione dell'energia è da includersi nel computo del lavoro dissipato, quindi in quei 900J. Magari mi sbaglio però
