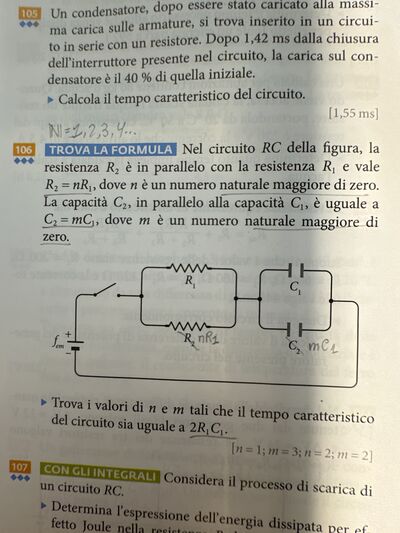
Nel circuito $R C$ della figura, la resistenza $R_2$ è in parallelo con la resistenza $R_1$ e vale $R_2=n R_1$, dove $n$ è un numero naturale maggiore di zero. La capacità $C_2$, in parallelo alla capacità $C_1$, è uguale a $C_2=m C_1$, dove $m$ è un numero naturale maggiore $\mathrm{di}$ zero.
Trova i valori di $n$ e $m$ tali che il tempo caratteristico del circuito sia uguale a $2 R_1 C_1$.
$$
[n=1 ; m=3 ; n=2 ; m=2]
$$
17
punti
Livello 0
R equivalente parallelo:
Re = (1/R1 + 1/nR1) ^-1;
Re = [(n + 1) /(nR1)]^-1;
Re = n R1 / (n + 1),
C equivalente parallelo:
Ce = C1 + m C1 = C1 (m + 1);
tempo caratteristico (tau τ) :
τ = Re * Ce;
Deve essere:
Re * Ce = 2 R1 C1;
[n R1 / (n + 1)] * [C1 (m + 1)] = 2 R1 C1 ;
[n / (n + 1)] * [(m + 1)] * R1 C1 = 2 R1 C1;
[n / (n + 1)] * [(m + 1)] = 2
[n * (m + 1) / (n + 1)] = 2;
n * (m + 1) = 2 * (n + 1);
n m + n = 2 n + 2;
n m = 2n - n + 2;
n m = n + 2;
n m - n = 2;
n * (m - 1) = 2;
m - 1 = 2 / n;
m = 2/n + 1; m ed n devono essere interi;
n = 1;
m = 2/1 + 1 = 3;
n = 2;
m = 2/2 + 1 = 2.
74863
punti
Genius II
