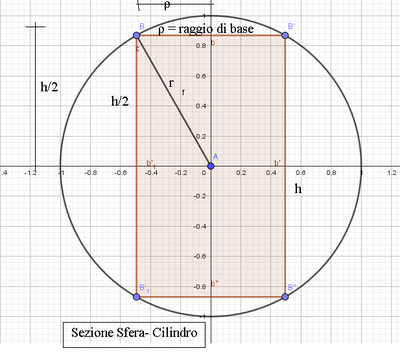
Buona giornata e buon anno a tutti; vado a postare il seguente problema : un cilindro è inscritto in una sfera di raggio r. Calcolare la misura del raggio di base e quella dell'altezza del cilindro, sapendo che la superficie della sfera è 169/90 della superficie laterale del cilindro. Risposte : raggio di base 1 = 5/13r; h1= 24/13r raggio di base2 = 12/13r; h2= 10/13r. Chiedo gentilmente lo svolgimento passaggio per passaggio e il disegno dei 2 solidi per comprendere meglio l'esercizio. Grazie a tutti coloro che vorranno rispondermi.