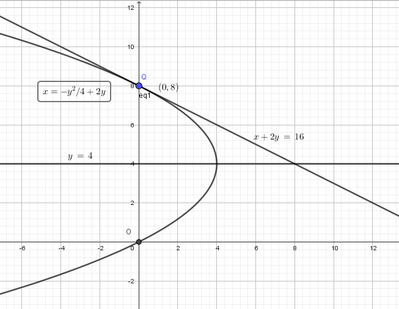
a. Scrivi l'equazione della parabola tangente alla retta $x+2 y-16=0$ nel suo punto di intersezione con lasse delle ordinate e avente per asse di simmetria la retta $y-4=0$.
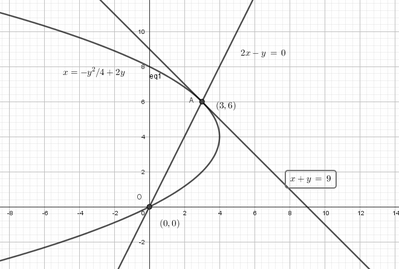
b. La retta $2 x-y=0$ interseca la parabola nell'origine $O$ e nel punto $A$. Scrivi l'equazione della retta $r \tan$ gente alla parabola in $A$.
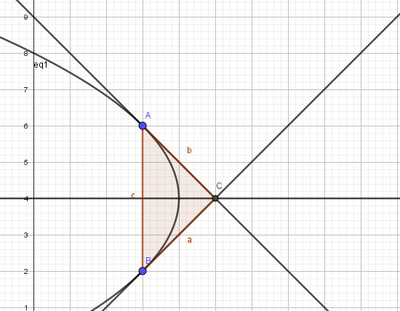
c. Determina l'equazione della retta $s$ simmetrica della retta $r$ rispetto all'asse di simmetria della parabola e dimostra che anche la retta $s$ è tangente alla parabola in un punto $B$ di cui si chiedono le coordinate.
d. Sia $C$ il punto di intersezione tra le rette $r$ e $s$. Calcola l'area della figura che ha come lati $A C$ e $C B$ e l'arco di parabola $A B$.
$$
\left[\text { a) } x=-\frac{1}{4} y^2+2 y \text {; b) } x+y-9=0 \text {; c) } x-y-1=0, B(3 ; 2) \text {; d) } \frac{4}{3}\right]
$$