Vi chiedo gentilmente di aiutarmi con questo problema, se non è un problema potreste farlo su un foglio e allegare una foto dal momento che è abbastanza lungo?
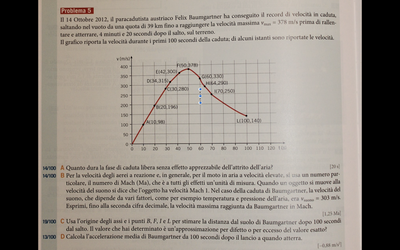
Il 14 Ottobre 2012, il paracadutista austriaco Felix Baumgartner ha conseguito il record di velocità in caduta,
saltando nel vuoto da una quota di 39 km fino a raggiungere la velocità massima Vmax = 378 m/s prima di rallentare e atterrare, 4 minuti e 20 secondi dopo il salto, sul terreno.
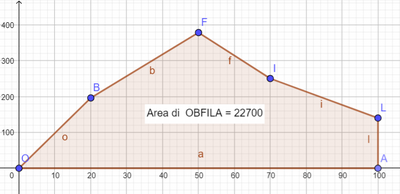
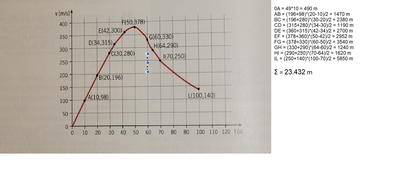
Il grafico riporta la velocità durante i primi 100 secondi della caduta; di alcuni istanti sono riportate le velocità.
qui sopra il grafico ^^
A Quanto dura la fase di caduta libera senza effetto apprezzabile dell'attrito dell'aria?
(20 s)
B Per la velocità degli aerei a reazione e, in generale, per il moto in aria a velocità elevate, si usa un numero particolare, il numero di Mach (Ma), che è a tutti gli effetti un'unità di misura. Quando un oggetto si muove alla velocità del suono si dice che l'oggetto ha velocità Mach 1. Nel caso della caduta di Baumgartner, la velocità del suono, che dipende da vari fattori, come per esempio temperatura e pressione dell'aria, era v(suono) =303 m/s. Esprimi, fino alla seconda cifra decimale, la velocità massima raggiunta da Baumgartner in Mach.
(1,25 Ma)
C Usa l'origine degli assi e i punti B, F, Ie L per stimare la distanza dal suolo di Baumgartner dopo 100 secondi dal salto. Il valore che hai determinato è un'approssimazione per difetto o per eccesso del valore esatto?
D Calcola l'accelerazione media di Baumgartner da 100 secondi dopo il lancio a quando atterra.
(-0,88 m/s^2)