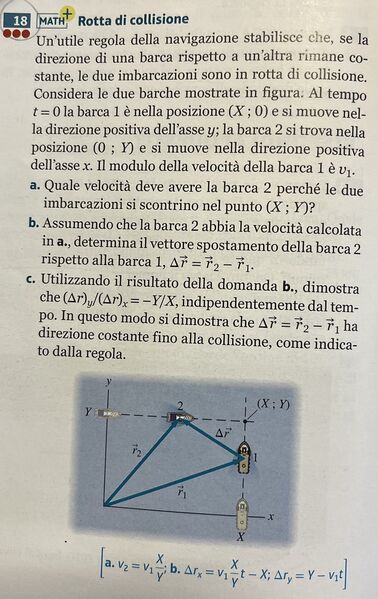
Un'utile regola della navigazione stabilisce che, se la direzione di una barca rispetto a un'altra rimane costante, le due imbarcazioni sono in rotta di collisione. Considera le due barche mostrate in figura: $\mathrm{Al}$ tempo $t=0$ la barca 1 è nella posizione $(X ; 0)$ e si muove nella direzione positiva dell'asse $y$; la barca 2 si trova nella posizione $(0 ; Y)$ e si muove nella direzione positiva dell'asse $x$. Il modulo della velocità della barca 1 è $v_1$.
a. Quale velocità deve avere la barca 2 perché le due imbarcazioni si scontrino nel punto $(X ; Y)$ ?
b. Assumendo che la barca 2 abbia la velocità calcolata in a., determina il vettore spostamento della barca 2 rispetto alla barca $1, \Delta \vec{r}=\vec{r}_2-\vec{r}_1$.
c. Utilizzando il risultato della domanda b., dimostra che $(\Delta r)_y /(\Delta r)_x=-Y / X$, indipendentemente dal tempo. In questo modo si dimostra che $\Delta \vec{r}=\vec{r}_2-\vec{r}_1$ ha direzione costante fino alla collisione, come indicato dalla regola.
non riesco a fare il punto b!