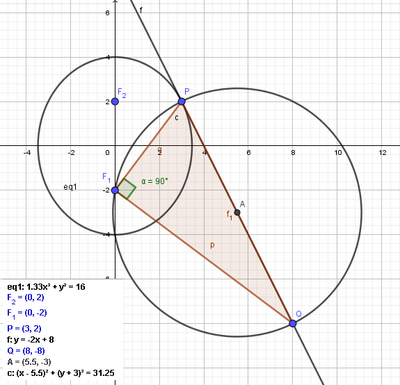
L'ellisse della figura ha eccentricità. 1/2
e i fuochi in F1 e F2.
a. Determina l'equazione dell'ellisse e scrivi l'equazione della tangente t nel suo punto P di ascissa 3.
b. Detto Q il punto di intersezione di t con la retta di equazione
y =-8, verifica che l'angolo PF1Q è retto e scrivi l'equazione della circonferenza circoscritta al triangolo PEQ.
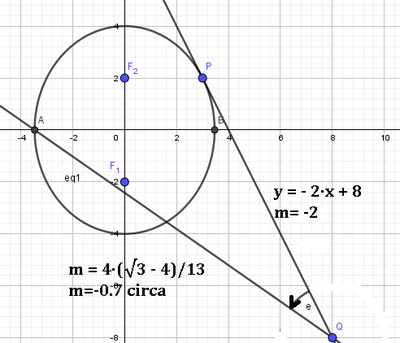
Considera tutte le rette passanti per Q e trova per quali valori
del coefficiente angolare intersecano l'arco AB di ellisse che si
trova nel semipiano y > 0.