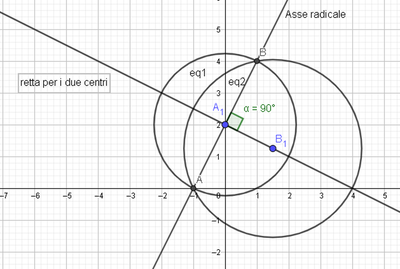
Volevo completare quanto ho già detto in precedenza.
La posizione reciproca di due luoghi geometrici consiste nel vedere se sono verificate le seguenti condizioni: a) i due luoghi geometrici si intersecano in uno o più punti; b) sono tra loro tangenti in qualche punto; c) non si intersecano in alcun punto.
Nel nostro caso abbiamo due circonferenze. Se le mettiamo a sistema si ottiene per differenza:
{x^2 + y^2 - 4·y - 1 = 0
{x^2 + y^2 - 3·x - 5·y/2 - 4 = 0
----------------------------------
3·x - 3·y/2 + 3 = 0 ossia y = 2·x + 2
Ora deve essere chiaro che la soluzione del sistema:
{x^2 + y^2 - 4·y - 1 = 0
{y = 2·x + 2
porta ad una equazione di secondo grado:
x^2 + (2·x + 2)^2 - 4·(2·x + 2) - 1 = 0
x^2 + (4·x^2 + 8·x + 4) - (8·x + 8) - 1 = 0
5·x^2 - 5 = 0
In tal caso abbiamo un'equazione pura che ha:
Δ = b^2 - 4·a·c --->Δ = 0^2 - 4·5·(-5)--->Δ = 100 >0 e quindi 2 radici reali e distinte.
Quindi le due circonferenze si intersecano in due punti.
5·(x + 1)·(x - 1) = 0---->x = -1 ∨ x = 1
Per x=-1:
y = 2·(-1) + 2---->A(-1,0)
Analogamente :
y = 2·1 + 2 ---> B(1,4)
e per tali punti passa l'asse radicale.