Ci sono due sole possibilità, e nessuna di esse rientra nella categoria "matematica creativa".
Può trattarsi di "matematica RIcreativa": Da dov'è che viene il quadretto in più? Ah, ah, bello il trucco grafico! Che pazienza a costruirlo, bravo!
Oppure può trattarsi, più probabilmente, di una "domanda trabocchetto" di quelle che si fanno agli alunni più brillanti per vedere se azzeccano il "pensiero laterale" e gli si può alzare il voto.
------------------------------
Nell'esercizio ci sono un paio di dati di fatto e un po' di trucchi.
---------------
Fatti
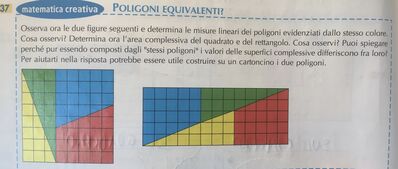
* un quadrato di lato L = 8 ha area Q = L^2 = 64.
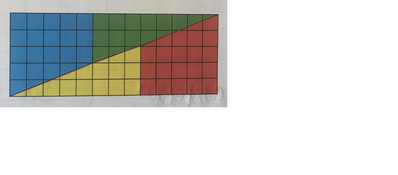
* un rettangolo di base b = 13 e altezza h = 5 ha area R = b*h = 65.
---------------
Trucco #1 (verbale)
La domanda «Puoi spiegare perché, pur essendo composti dagli "stessi poligoni", i valori delle superficie complessive differiscono fra loro?» è un bell'esempio di menzogna occulta.
Dal momento che le aree sono differenti, è falso affermare che siano composti dagli "stessi poligoni".
---------------
Trucco #2 (grafico)
Nel rettangolo c'è un poligono in più, così lungo da mimetizzarsi nello spessore della linea tracciata lungo la diagonale.
---------------
Trucco #3 (didattico, ma un po' fuorviante)
Il suggerimento di usare un cartoncino per i due poligoni.
------------------------------
COME EVIDENZIARE IL POLIGONO MIMETIZZATO
Su un foglio a quadrettoni (i più grandi possibile, se non lo trovi disegnalo da te tracciando a matita ogni quadrettone fatto di tre per tre quadrettini) disegna I SOLI CONTORNI del quadrato otto per otto e del rettangolo tredici per cinque. Poi disegni le linee interne del solo quadrato per ritagliarne i due trapezi e i due triangoli componenti. Infine disponi i pezzi ritagliati nel contorno del rettangolo allineandoli accuratamente ai bordi.
Se i quadrettoni sono abbastanza grandi e se l'allineamento è abbastanza accurato vedrai che lungo la diagonale resta scoperto un poligono sottile che devi colorare di nero per poterlo poi esibire in classe.