Due corpi $A$ e $B$ hanno masse rispettivamente di $8,00 \mathrm{~kg}$ e $2,00 \mathrm{~kg}$ e sono disposte come in figura. Sapendo che il piano è inclinato di $30^{\circ}$ e che l'attrito lungo il piano è trascurabile, determina il modulo dell'accelerazione del corpo $A$ lungo il piano inclinato. Cosa cambia se la massa del corpo $B$ è pari a $4,00 \mathrm{~kg}$ ?
42
punti
Livello 0
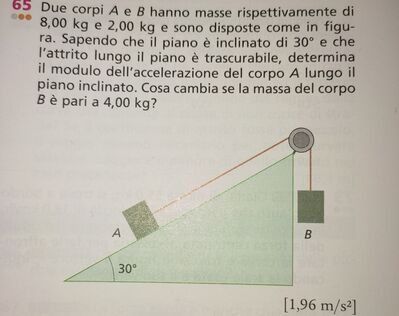
Sul corpo A agiscono due forze: la forza parallela al piano F// = mA * g * sen30° verso il basso e la Forza di tensione T del filo che tira il corpo verso l'alto del piano.
F// = 8,00 * 9,8 * 0,5 = 39,2 N;
Sul corpo B agisce il suo peso FB = mB * g, verso il basso e la tensione T del filo verso l'alto.
Non considerando la tensione, vediamo però che le due forze F// e F peso sono contrarie, F// da una parte e FB dalla parte opposta.
Fpeso = 2,00 * 9,8 = 19,6 N;
F// > FB, quindi il corpo A scende lungo il piano e trascina il corpo B verso l'alto:
F ris = F// - FB = 39,2 - 19,6 = 19,6 N;
a = F ris / (mA + mB);
a = 19,6 / (2,00 + 8,00) = 19,6 / 10,00;
a = 1,96 m/s^2; accelerazione, il corpo A scende il corpo B sale.
Se B diventa 4,00 kg;
FB = 4 * 9,8 = 39,2 N;
F// - FB = 0 N;
il sistema è in equilibrio.
La forza risultante è 0 N, l'accelerazione è 0 m/s^2.
Il sistema se è già in movimento, si muoverà a velocità costante.
ciao @skander
74873
punti
Genius II
