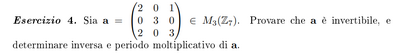Salve come da titolo vorrei ricavare il periodo della seguente matrice.
Esercizio 4. Sia a $=\left(\begin{array}{lll}2 & 0 & 1 \\ 0 & 3 & 0 \\ 2 & 0 & 3\end{array}\right) \in M_3\left( Z _7\right)$. Provare che a è invertibile, e determinare inversa e periodo moltiplicativo di a.
Sono arrivato fino ad a^4 ma niente, c'è un modo per procedere più velocemente?
103
punti
Livello 1
* A = {{2, 0, 1}, {0, 3, 0}, {2, 0, 3}}
* det[A] mod 7 = 12 mod 7 = 5 != 0 ≡ A è invertibile
* inv[A] mod 7 = ({{9, 0, - 3}, {0, 4, 0}, {- 6, 0, 6}})/12 mod 7 =
= ({{2, 0, 4}, {0, 4, 0}, {1, 0, 6}})*(inv[12 mod 7] mod 7) =
= ({{2, 0, 4}, {0, 4, 0}, {1, 0, 6}}*3 mod 7 =
= {{6, 0, 12}, {0, 12, 0}, {1, 0, 18}} mod 7 =
= {{6, 0, 5}, {0, 5, 0}, {1, 0, 4}}
---------------
* A^1 mod 7 = {{2, 0, 1}, {0, 3, 0}, {2, 0, 3}} != I
* A^2 mod 7 = {{6, 0, 5}, {0, 2, 0}, {3, 0, 4}} != I
* A^3 mod 7 = {{1, 0, 0}, {0, 6, 0}, {0, 0, 1}} != I
* A^4 mod 7 = {{6, 0, 5}, {0, 5, 0}, {3, 0, 4}} != I
* A^5 mod 7 = {{6, 0, 5}, {0, 5, 0}, {3, 0, 4}} != I
* A^6 mod 7 = {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} = I
---------------
"c'è un modo per procedere più velocemente?"
Ma certo che c'è, si chiama uso del software: prova a immettere il comando
Mod[MatrixPower[{{2,0,1},{0,3,0},{2,0,3}},k],7]
nella casella di testo di www.wolframalpha.com e vedi che cosa ottieni.
Poi ti basta risolvere per quel k che azzera i valori non diagonali e rende uno i diagonali.
57382
punti
Genius I
