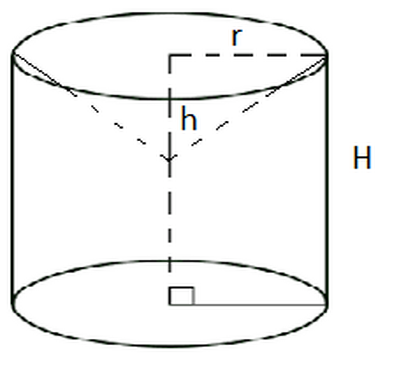
In un cilindro equilatero di bronzo $(P s=8,75)$ il cui raggio misura $12 \mathrm{~cm}$, è stato scavato un cono, con la base coincidente con quella del cilindro, alto $5 \mathrm{~cm}$. Calcola l'area della superficie totale, il volume ed il peso del solido.
$$
\left[876 \pi \mathrm{cm}^2=2750,64 \mathrm{~cm}^2 ; 3216 \pi \mathrm{cm}^3=10098,24 \mathrm{~cm}^3, 88359,6 \mathrm{~g}\right]
$$
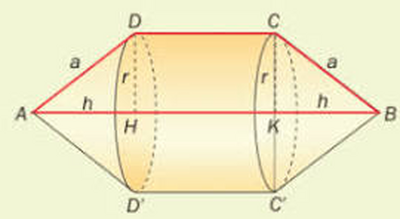
Un solido è costituito da un cilindro equilatero e da due coni congruenti aventi le basi coincidenti con quelle del cilindro. Calcola l'area della superficie totale del solido sapendo che la circonferenza di base è lunga $36 \pi \mathrm{cm}$ e il volume del solido è $16848 \pi \mathrm{cm}^3$.
$\left[2376 \pi \mathrm{cm}^2=7460,64 \mathrm{~cm}^2\right]$
Avrei bisogno del n. 206
Grazieee