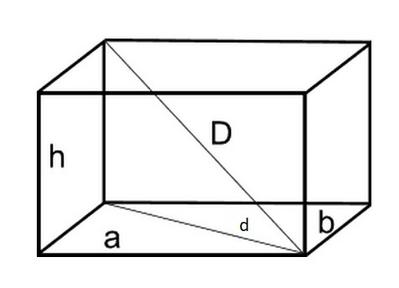
La diagonale del parallelepipedo rettangolo misura 29 cm, il perimetro della base è 56 cm e le dimensioni di base sono una 3/4 dell'altra. Calcola il volume e la massa in kilogrammi del solido, supponendo che sia di vetro. Grazie per l'aiuto che mi darete