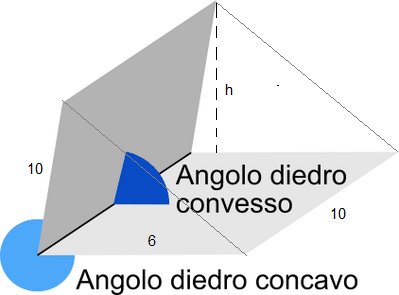
Un parallelepipedo a base rettangolare $A B C D$ è tale che una faccia laterale forma con il piano di base un diedro di ampiezza $x$ e ilo spigolo laterale è lungo quanto la dimensione maggiore del rettangólo. La somma delle dimensioni del rettangolo di base è 16 dm e una dimensione è $\mathrm{i} \frac{5}{3}$ dell'altra. Determina l'ampiezza dell'angolo $x$ in modo tale che il volume del parallelepipedo $300 \sqrt{2} \mathrm{dm}^3$
PER FAVORE CHI MI AIUTA A FARE LA FIGURA DI QUESTO PROBLEMA?
385
punti
Livello 2
Lo spigolo laterale (lunghezza congruente alla dimensione maggiore di base) è l'ipotenusa di un triangolo rettangolo avente uno dei cateti congruente con l'altezza del solido e opposto all'angolo di x gradi. Le misure di base sono:
d1= 10 dm
d2 = 6 dm
Quindi lo spigolo laterale è 10 dm
Possiamo calcolare l'altezza del solido:
H= 10* sin(x)
Il volume del solido è:
V= S_base * h = 60*10*10 sin(x) = 600*sin(x) dm³
Imponendo la condizione:
V= 300*radice (2)
si ottiene:
600 sin(x) = 300*radice (2)
sin(x) = radice (2) /2
x= 45 gradi
Possibilmente cerca di allegare delle foto un pó più LEGGIBILI... ogni volta è una fatica leggere il testo. Grazie. Buona giornata
76754
punti
Genius II
la forma è quella mostrata sopra
300√2 = 6*1*h/2
h = 600√2/60 = 10√2....qualcosa non va nei dati
114462
punti
Genius II
