Determina la parabola simmetrica di y = x^2 rispetto:
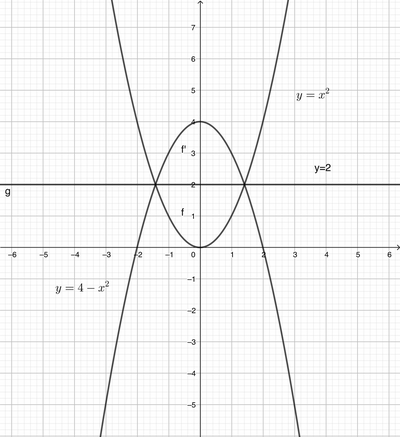
a. Alla retta y = 2;
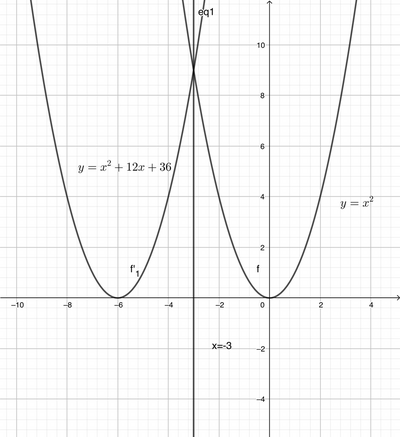
b. Alla retta x = -3;
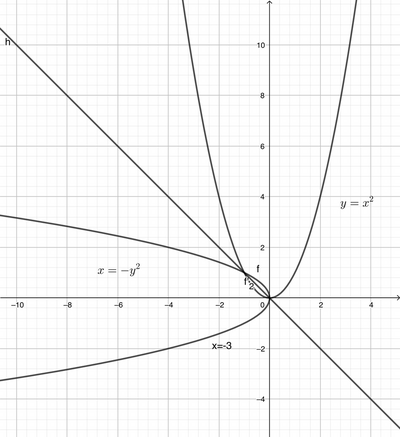
c. Alla bisettrice del secondo e quarto quadrante;
d. All’asse x;
e. All’asse y.
risultati: a. y = -x^2 + 4; b. y = (x + 6)^2; c. x = -y^2; d. y = -x^2; e. y = x^2.
46
punti
Livello 0
Qualcuno mi potrebbe aiutare?
I punti d) ed e) sono semplici.
Visto il commento rispondo per i tre casi esaminati di figura.
y = x^2 parabola da trasformare per ottenere la simmetrica assiale.
rispetto alla retta y=2 la x non cambia cambia la y:
y ----> 2·2 - x^2-----> y = 4 - x^2
Rispetto alla retta x=-3, la y non cambia, cambia la x:
x ---> 2·(-3) - x-------> x ------> -x - 6 (fai la sostituzione indicata)
y = (-x - 6)^2-------> y = x^2 + 12·x + 36
Il terzo caso opera le sostituzioni:
x------>-y
y------->-x
-x=(-y)^2------> -x=y^2 ossia x=-y^2
94643
punti
Genius II
@lucianop grazie Luciano ma non ho ancora risolto il mio problema, forse mi sono espresso male. Chiedevo i calcoli per riuscire a determinare l’equazione della parabola simmetrica.
