[Risolto] parabola

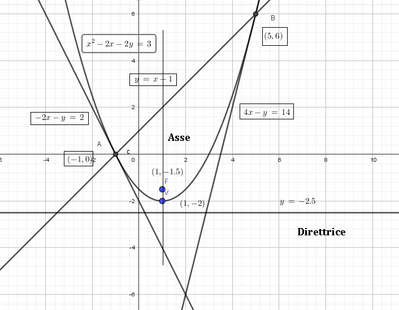
Fuoco e vertice hanno stessa ascissa => parabola con asse // asse y e direttrice y= - 5/2

La parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso F detto fuoco e da una retta detta d direttrice. Quindi anche V è equidistante da F e d

(x-1)²+(y+3/2)²=(y+5/2)²

Presa per buona l'equazione della parabola... 

Non credo tu abbia problemi a determinare i punti di intersezione A, B

Utilizziamo poi le formule di sdoppiamento per determinare il valore del coefficiente angolare della retta tangente la conica nel punto x0

m=2*a*x0 +b = 2*(1/2)*x0 - 1 = x0 - 1

m=x0 - 1

(x0 ascissa di A e B) 

L'intersezione tra la retta e la parabola permette di determinare le coordinate dei punti A. B

A( - 1;0) B(5;6)

Quindi:

mA= - 2 ; mB= 4

Noti i coefficienti angolari scriviamo l'equazione delle rette per A e B aventi coefficienti angolari ricavati in precedenza 

A) I due dati, fuoco F(1, - 3/2) e vertice V(1, - 2), implicano
* asse di simmetria x = 1
* distanza focale f = |Vd| = |VF| = 1/2 = 1/(4*|a|) → |a| = 1/2
* yF > yV → concavità verso y > 0 → apertura a = 1/2
* equazione richiesta
** Γ ≡ y = yV + a*(x - xV)^2 ≡ y = (x - 1)^2/2 - 2 ≡ x^2 - 2*x - 2*y - 3 = 0
---------------
B) (y = x + 1) & (y = (x - 1)^2/2 - 2) ≡ A(- 1, 0) oppure B(5, 6)
---------------
C1) A(- 1, 0): x*(- 1) - 2*(x + (- 1))/2 - 2*(y + 0)/2 - 3 = 0 ≡ y = - 2*(x + 1)
---------------
C2) B(5, 6): x*5 - 2*(x + 5)/2 - 2*(y + 6)/2 - 3 = 0 ≡ y = 2*(2*x - 7)