[Risolto] parabola

Intanto un disegno:

La parabola è del tipo: y = a·x^2 + b·x + c

In questo caso la scriviamo come:

y = a·(x + 1)·(x - 3)

ed imponiamo il passaggio per il punto P(2,3):

3 = a·(2 + 1)·(2 - 3)-------> a = -1

quindi la parabola è:

y = (-1)·(x + 1)·(x - 3)--------> y = - x^2 + 2·x + 3

Α = 21/4 = 5.25 area rettangolo richiesto

Metto a sistema:

{y = - x^2 + 2·x + 3

{y = k

Lo risolvo ed ottengo: [x = √(4 - k) + 1 ∧ y = k, x = 1 - √(4 - k) ∧ y = k]

Il rettangolo richiesto ha base:

b = √(4 - k) + 1 - (1 - √(4 - k))

b = 2·√(4 - k)

Quindi: Α = b·k = 21/4

2·k·√(4 - k) = 21/4

risolvo ed ottengo:

k = 3·√37/8 + 9/8 ∨ k = 7/4

(k = 3.406035948 ∨ k = 1.75)

In figura una delle due possibilità (la seconda)

L'equazione si può scrivere come

y = a( x+1)(x-3)

con 3 = a*3*(-1)

a = - 1

y = - x^2 +2x+3

Il resto lo svolgo più tardi. 

Se y = k é la retta su cui si trova l'altro lato 

- x^2 + 2x + 3 = k 

x^2 - 2x + k - 3 = 0 

la lunghezza della corda intercettata sulla parabola é

|x2 - x1| = rad(D)/|A| = rad(4 - 4(k - 3)) = rad (16 - 4k) = 2 rad(4 - k) 

con k <= 4

per cui la risolvente é 

2k rad(4 - k) = 21/4

8k rad (4 - k) = 21 

64 k^2 ( 4 - k ) = 441 

64 k^3 - 256 k^2 + 441 = 0

che si risolve per via iterativa o grafica 

o con la regola di Ruffini generalizzata 

una radice utile é k = 7/4

l'altra é k = 3.41 circa

Avendo già dati gli zeri X1(- 1, 0) e X2(3, 0) si scrive l'equazione della parabola Γ, con asse parallelo all'asse y, a meno dell'apertura "a" che si determina dal vincolo d'appartenenza di P(2, 3)
* Γ ≡ y = a*(x + 1)*(x - 3)
* 3 = a*(2 + 1)*(2 - 3) ≡ a = - 1
da cui la risposta a "Scrivi l'equazione ..." è
* Γ ≡ y = - (x + 1)*(x - 3) ≡ y = 4 - (x - 1)^2
con
* asse di simmetria x = 1
* vertice V(1, 4)
------------------------------
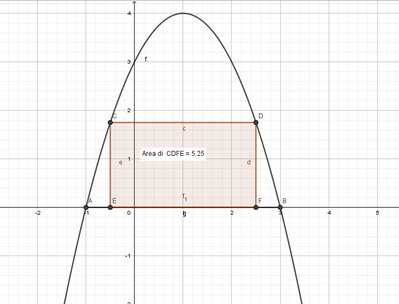
Ogni rettangolo inscritto come quello richiesto ha vertici
* A(1 - k, 0), B(1 + k, 0), C(1 + k, 4 - k^2), D(1 - k, 4 - k^2)
e area
* S(ABCD) = S(k) = |AB|*|BC| = 2k*(4 - k^2)
da cui il sistema risolutivo
* (S(k) = 21/4 = 2k*(4 - k^2)) & (0 < k < 2) ≡
≡ (k^3 - 4*k + 21/8 = 0) & (0 < k < 2) ≡
≡ ((k - 3/2)*(k^2 + (3/2)*k - 7/4) = 0) & (0 < k < 2) ≡
≡ (k = 3/2) oppure (k = (√37 - 3)/4 ~= 0.771)
pertanto ci sono due rettangoli che soddisfanno ai requisiti con i vertici
* A(- 1/2, 0), B(5/2, 0), C(5/2, 7/4), D(- 1/2, 7/4)
oppure
* A((7 - √37)/4, 0), B((1 + √37)/4, 0), C((1 + √37)/4, (3/8)*(3 + √37)), D((7 - √37)/4, (3/8)*(3 + √37))