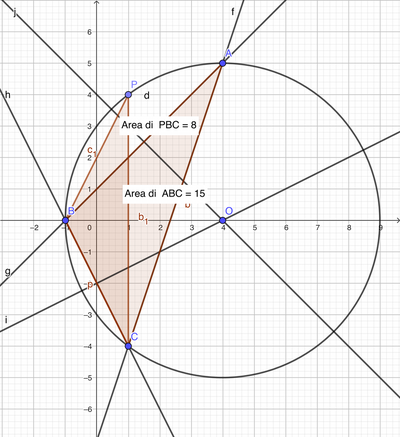
Calcola l'equazione della circonferenza circoscritta al triangolo i cui lati giacciono sulle rette di equazioni $y=3 x-7, y=x+1$ e $y=-2 x-2$. Indicato con $A$ il vertice del triangolo che si trova nel I quadrante e con B quello che si trova sull'asse $x$, determina sul minore degli archi $\overparen{A B}$ un punto $P$ in modo che l'area di $P B C>$ sia gli $\frac{8}{15}$ dell'area di $A B C$.
$$
\left[x^2+y^2-8 x-9=0 ; P(1 ; 4)\right]
$$
buongiorno, potete risolvermi per favore questo problema? grazie mille