n407

Question

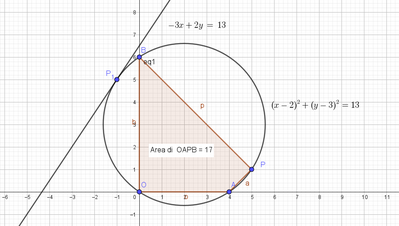
Scrivi l'equazione della circonferenza  gamma passante per l'origine O e tangente alla retta di equazione -3 x+2 y-13=0 nel suo punto di ascissa -1 .Detti A e B i punti di intersezione di  gamma con gli assi cartesiani, determina un punto P sulla semicirconferenza che non contiene l'origine in modo che l'area del quadrilatero O A P B sia uguale a 17.  left [x^2+y^2-4 x-6 y=0 ; P_1(5 ; 1), P_2( frac {17}{13} ;  frac {85}{13}) right ]  [attach]66611[/attach] salve, potete risolvermi questo problema? grazie mille

LucianoP · Accepted Answer

x^2 + y^2 + a·x + b·y = 0

- 3·x + 2·y - 13 = 0

Quindi la circonferenza per l'origine passa per il punto di tangenza:

x=1: - 3·(-1) + 2·y - 13 = 0---> 2·y - 10 = 0---> y = 5

[-1, 5]

per sostituzione:

(-1)^2 + 5^2 + a·(-1) + b·5 = 0

-a + 5·b + 26 = 0

a = 5·b + 26

Metto a sistema la circonferenza parametrica nella sola b:

{x^2 + y^2 + x·(5·b + 26) + b·y = 0

{- 3·x + 2·y - 13 = 0

procedo per sostituzione:

y = (3·x + 13)/2

x^2 + ((3·x + 13)/2)^2 + x·(5·b + 26) + b·((3·x + 13)/2) = 0

13·x^2/4 + 13·x·(b + 7)/2 + 13·(2·b + 13)/4 = 0

13·x^2 + 26·x·(b + 7) + 13·(2·b + 13) = 0

Δ/4 = 0 condizione di tangenza

(13·(b + 7))^2 - 13^2·(2·b + 13) = 0

169·b^2 + 2028·b + 6084 = 0

169·(b + 6)^2 = 0----> b = -6

x^2 + y^2 + (5·(-6) + 26)·x + (-6)·y = 0

x^2 + y^2 - 4·x - 6·y = 0

anche:

[2, 3]

r = √(2^2 + 3^2 - 0)---> r = √13

(x - 2)^2 + (y - 3)^2 = 13

LucianoP

(@lucianop)

78829 punti

livello:

Genius II

14392 Risposte
5 7434 2934

12/01/2024 17:22

[Risolto] n407

Domande