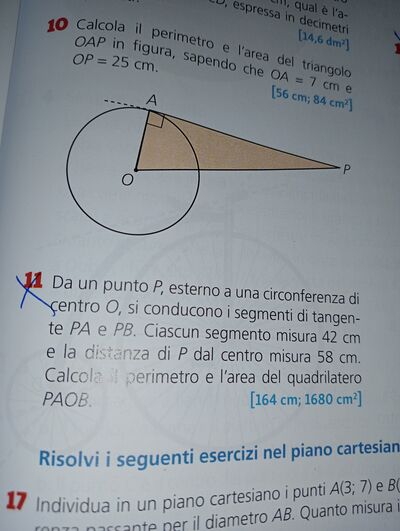
Da un punto $P$, esterno a una circonferenza di çentro $O$, si conducono i segmenti di tangente $P A$ e $P B$. Ciascun segmento misura $42 cm$ e la distanza di $P$ dal centro misura $58 cm$. Calcola il perimetro e l'area del quadrilatero $P A O B$
$\left[164 cm ; 1680 cm ^2\right]$
24
punti
Livello 0
La distanza del punto P dal centro della circonferenza è l'ipotenusa di un triangolo rettangolo avente come cateti il raggio e il segmento di tangenza.
Teorema di Pitagora. Determino il raggio
R=radice (58² - 42²) = 40 cm
I segmenti di tangenza condotti dal punto esterno alla conica sono congruenti.
Quindi
2p = 2R+2*PA = 80 + 84 = 164 cm
A= R*PA = 40*42 = 1680 cm²
76753
punti
Genius II
