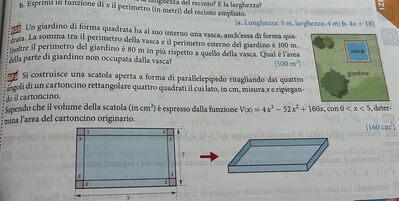
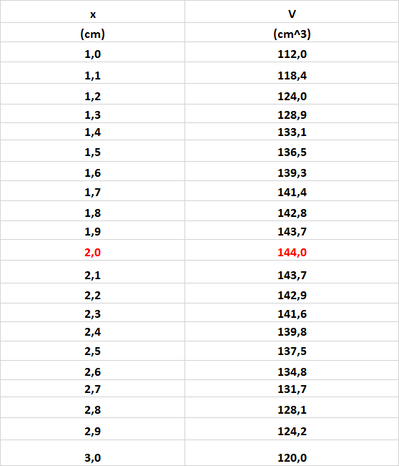
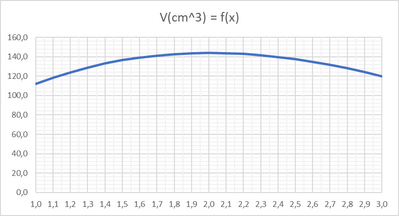
Si costruisce una scatola aperta a forma di parallelepipedo ritagliando dai quattro angoli di un cartoncino rettangolare quattro quadrati il cui lato, in $\mathrm{cm}$, misura $x$ e ripiegando il cartoncino.
Sapendo che il volume della scatola (in $\mathrm{cm}^3$ ) è espresso dalla funzione $V(x)=4 x^3-52 x^2+160 x$, con $0<x<5$, determina l'area del cartoncino originario.
37
punti
Livello 0
volume V = (a-2x)*(b-2x)*x = 4x^3-52x^2+160x
(ab-2bx-2ax+4x^2)*x = 4x^3-52x^2+160x
si semplifica per x
ab-2bx-2ax+4x^2 = 4x^2-52x+160
4x^2 si elide
-2x(a+b)+ab = -52x+160
ab = 160
a+b = 26
a = 16 ; b = 10
qual è l'x che massimizza il volume?
114464
punti
Genius II
