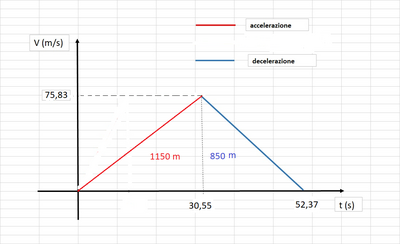
a1 = 2,5 m/s^2:
a2 = - 3,5 m/s^2
S1 = 1/2 * (+ 2,5) * t1^2;
la velocità cresce nel tempo t1
v1 = 2,5 * t1; ( v1 è la velocità iniziale vo per il secondo tratto
S2 = 1/2 * (- 3,5) * t2^2 + v1 * t2 ;
S2 = 1/2 * (- 3,5) * t2^2 + 2,5 t1 * t2 ;
S1 + S2 = 2000 m;
v2 finale = 0;
v2 = - 3,5 * t2 + vo
v2 = - 3,5 * t2 + 2,5 * t1 ;
- 3,5 * t2 + 2,5 * t1 = 0; si ferma;
t1 / t2 = 3,5 / 2,5;
t1 = 1,4 t2;
S1 + S2 = 2000;
1/2 * (+ 2,5) * t1^2 + 1/2 * (- 3,5) * t2^2 + 2,5 t1* t2 = 2000;
1,25 (1,4 t2)^2 - 1,75 * (t2)^2 + 2,5 * (1,4 t2) * t2 = 2000;
2,45 (t2)^2 - 1,75 t2^2 + 3,5 t2^2 = 2000;
4,2 t2^2 = 2000;
t2 = rad(2000 / 4,2) = 21,8 s;
t1 = 1,4 * 21,8 = 30,6 s.
T = t1 + t2 = 30,6 + 21,8 = 52,4 s;
Tempo totale massimo = 52 secondi circa.
Avevo sbagliato i calcoli. Ho ricalcolato.
Ciao @andrea_bergamini