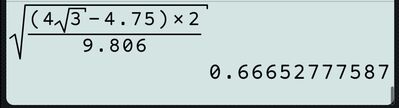[Risolto] Moto parabolico, 3 stelle difficile

x = 4,00 m; y = 6,00 m;

vox = vo * cos60°= vo * 0,5;

voy = vo * sen60°= vo * 0,866;

x = vox * t;    (1)

y = 1/2 * g * t^2 + voy * t + yo;  (2)

(vo * 0,5) * t = 4,00;   ricaviamo vo e lo sostituiamo nella (2);

vo = 4,00 /(0,5  t);  (1)

vo = 8,00 / t

1/2 * (-9,8) * t^2 + (0,866 * vo) * t + 1,25 = 6,00;   (2)

- 4,9 * t^2 + (0,866 * 8,00/t) * t = 6,00 - 1,25;

- 4,9 t^2 + 6,928 = 4,75 ;

- 4,9 t^2 = 4,75 - 6,928;

4,9 t^2 = 2,178;

t^2 = 2,178 /4,9 = 0,444;

t = radice quadrata(0,444) = 0,667 s; (tempo impiegato dalla palla per arrivare a  6,00 m e percorrere in orizzontale  x =  4,00 m).

vo = 4,00 /(0,5  t);  (1)

vo = 4,00 / (0,5 * 0,667) = 12,0 m/s.

Devo finire, è lunga la storia....

Troviamo il tempo che la palla impiega ad  arrivare a y = 0,800 m da terra al di là della recinzione con la legge del moto verticale (2), poi con il tempo t trovato sapremo lo spostamento x orizzontale della palla.

voy = 12,0 * sen60° = 10,39 m/s; (velocità verticale di partenza).

y = 1/2 * g * t^2 + voy * t + yo;

0,800 = - 4,9 * t^2 + 10,39 * t + 1,25 ;

- 4,9 t^2 + 10,39 * t + 1,25 - 0,800 = 0 ; cambiando i segni:

4,9 t^2 - 10,39 t - 0,45 = 0;

t = [10,39 +- radice(10,39^2 + 4 * 4,9 * 0,45) ] / (2 *9,8);

t = [10,39 +- radice(116,77)]/9,8;

t = [10,39 +- 10,806]/9,8;

t = (10,39 + 10,806) /9,8 = 2,16 s; (tempo che la palla impiega per arrivare a 0,800 m da terra).

x = vox * t = (12 * 0,5) * 2,16 = 12,96 m;

Distanza dalla rete dalla parte di Mauro:

d = 12,96 - 4,00 = 8,96 m;

Mauro parte da 24 metri, deve percorre una spazio S per raggiungere la palla, nel tempo di 2,16 s:

S = 24 m - 8,96 = 15,04 m;

v = S / t = 15,04 / 2,16 = 6,96 m/s.

Ciao  @swaggyvioluz

Lungo l'asse x: moto rettilineo uniforme

x= v0_x * t = v0*cos (60)*t

Con x= 4m, cos (60)= 1/2 si ricava:

v0*t = 8

Lungo l'asse y: moto uniformemente accelerato 

h(t) = h0 + v0*sin(60)*t - (1/2)*g*t²

Con:

h(0)= 1,25 m

h(t) = 6 m (punto in cui sfiora la recinzione) 

si ricava:

h(t) - h0 = (v0*t) * sin(60) - (1/2)*g*t²

Ma: v0*t = 8 (dalla legge oraria lungo l'orizzontale) 

Quindi:

4.75 = 4*radice (3) - (1/2)*g*t²

Da cui si ricava l'unica soluzione accettabile:

t= 0,666 s

Tempo necessario a raggiungere la recinzione 

Sostituendo tale valore nella legge oraria del moto rettilineo uniforme si ricava:

v0= 0,666*8 = 12 m/s

Utilizziamo la legge oraria del moto uniformemente accelerato per determinare quanto tempo la palla impiega ad arrivare da Mauro. 

V0_y = 12* sin(60) = 6*radice (3)  m/s

h(t) = h0+ v0_y *t - (1/2)*g*t²

Con:

h0= 1,25 m

h(t) = 0,80 m

si ricava un'equazione di secondo grado in t. 

(1/2)*g*t² - 6*radice (3)*t - 0,45 = 0

Dalla soluzione dell'equazione si ricava l'unica soluzione accettabile:

t= 2,16 s

Tempo impiegato dalla pallina per giungere a Mauro 

Dalla legge oraria del moto lungo l'asse x determino la distanza percorsa dalla pallina in 2,16 s

V0_x = 6  m/s

d= 6*2,16 = 12,96 m

Mauro corre a velocità costante e deve percorrere uno spazio:

S= 24 - (12.96 - 4)

in un tempo

t= 2,16 s

Quindi: v= S/t = 6,96  m/s

moto orizzontale :

0,5*Vo*t = 4 m 

Vo = 8/t

moto verticale 

ho+Vo*0,866*t-g/2*t^2 = 6,0 m

1,25+8/t*0,866*t-4,903t^2 = 6

1,25+6,928-6 = 4,903t^2

t = √(1,25+6,928-6) / 4,903 = 0,666 sec 

Vo = 8/t = 8*3/2 = 12,0 m/sec 

moto verticale complessivo della pallina :

(0,80-1,25) = 12*0,866*t'-4,903t'^2

-0,45-10,39t'+4,903 tì^2 = 0 

tempo di volo t' = (10,39+√10,39^2+4*0,45*4,903)/9,806 = 2,1616 sec  

distanza orizzontale percorsa d' = Vo*0,5*t' = 6*2,1616 = 12,97 m 

velocità di intercetto V = (24+4-d')/t' = (28-12,97)/2,1616 = 6,953 m/sec