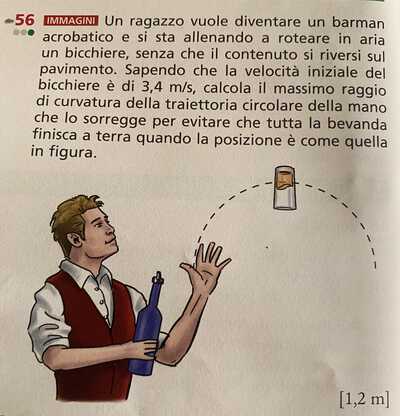
Un ragazzo vuole diventare un barman acrobatico e si sta allenando a roteare in aria un bicchiere, senza che il contenuto si riversi sul pavimento. Sapendo che la velocità iniziale del bicchiere è di $3,4 m / s$, calcola il massimo raggio di curvatura della traiettoria circolare della mano che lo sorregge per evitare che tutta la bevanda finisca a terra quando la posizione è come quella in figura.
Potete cortesemente aiutarmi in questo problema? Sto riscontrando difficoltà nella risoluzione
36
punti
Livello 0
L'accelerazione centrifuga non dev'essere minore di quella di gravità
* v^2/r >= g
quindi il raggio della trajettoria non dev'essere maggiore di v^2/g
* r <= v^2/g = (17/5)^2/(196133/20000) = 231200/196133 ~= 1.17879 m ~= 1.18 m
57382
punti
Genius I
L'idea è che per far in modo che l'acqua non cada devono bilanciarsi forza peso e centrifuga. Quindi m*v^2/r=m*g
96
punti
Livello 1
Deve essere m v^2/R >= m g
in modo che la forza centrifuga prevalga sulla forza peso
da cui v^2/g >= R => R <= v^2/g
così R max = 3.4^2 / 9.8 m = 1.18 m
47892
punti
Livello 7
ac = g = 9,806 = V^2/r
r > 3,4^2/9,806 > 1,18 m
114341
punti
Genius II
