Esercizio 129
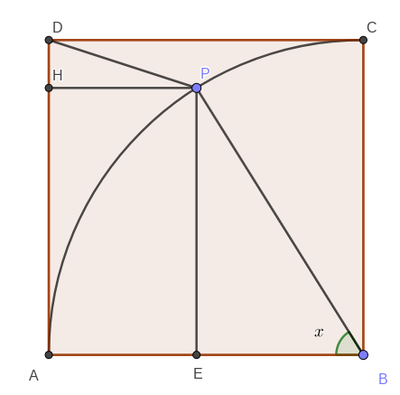
Nel quadrato ABCD, di lato lungo 1 m, traccia l’arco di circonferenza AC di centro B. Su di esso considera il punto P individuato dall’angolo $A\widehat{B} P=x$. Sia H la proiezione di P su AD.
a. Trova per quali valori di $x$ si ha $\overline{PD}^2=3-\sqrt{6} $
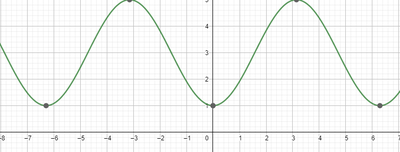
b. Traccia il grafico di $y=2 \cdot \overline{AB} \cdot \overline{AH}+\overline{PD}^2 in funzione di $x$.
Esercizio 130
Dato il segmento AB di lunghezza unitaria, considera la semiretta AP che forma con AB un angolo acuto PAB=x. Sia Q la proiezione di B su AP. Costruisci il triangolo AQC rettangolo e isoscele, di ipotenusa AQ, nel semipiano generato da AP non contenente B.
a. Determina i valori di x per cui l'area del quadrilatero ABQC risulta minore di $\frac{1}{4} $.
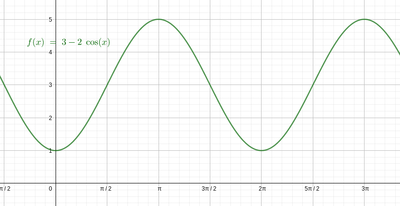
b. Considera la funzione f(x) che rappresenta l'area del triangolo ABQ, traccia il grafico limitatamente all'intervallo del problema goniometrico e individua il suo valore massimo.
Esercizio 131
Data la semicirconferenza di diametro AB=2r, siano P un punto di essa e H la proiezione di P sul diametro AB. Determina $f(x)=\frac{\overline{AH}+\overline{PH} }{\overline{HB}} $ in funzione dell'angolo PBA=x e calcola per quale valore di x si ha f(x)=2.