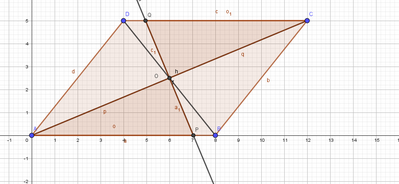
È dato un parallelogramma ABCD. L'asse della diagonale AC incontra il lato AB (o il suo prolungamento) in P e il lato CD (o il suo prolungamento) in Q. Dimostra che:
a. i triangoli AOP e QOC sono congruenti, essendo O il punto di intersezione delle diagonali di ABCD;
b. APCQ è un rombo.
14
punti
Livello 0
Per costruzione i triangoli AOP e OQC sono triangoli rettangoli congruenti fra loro in quanto hanno cateti AO ed OC congruenti ed angoli acuti uguali perché alterni interni . Quindi risulta pure QC=AP.
Il punto di intersezione O delle due diagonali è pure lo stesso di intersezione della diagonale AC con l'asse della stessa.
Il quadrilatero APCQ è un rombo in quanto le diagonali s ono ortogonali fra loro e si bisecano scambievolmente in virtù del teorema di Talete.
94792
punti
Genius II
