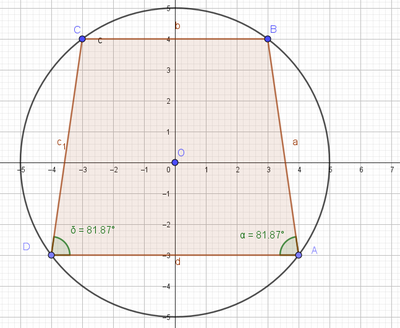
Due archi AB e CD di una circonferenza sono congruenti e non hanno punti in comune (i punti A, B, C e D si susseguono sulla circonferenza in quest'ordine). Dimostra che il quadrilatero ABCD è un trapezio isoscele. (Suggerimento: per dimostrare che BC || AD, ragiona su opportuni angoli alla circonferenza e utilizza il criterio di paralleli...
62
punti
Livello 1
Gli angoli α e δ sono angoli alla base AD del quadrilatero ABCD di figura.
Tali angoli sono congruenti in quanto alla circonferenza e sottesi ad archi congruenti BD e CA : lo sono perché somma di archi congruenti (in particolare BC è in comune).
Siccome gli angoli opposti di un quadrilatero inscritto ad una circonferenza sono supplementari, ne consegue che lo sono anche gli angoli δ e γ come pure α e β: ne consegue il parallelismo tra i lati AD e BC. Quindi ABCD è un trapezio (isoscele).
94774
punti
Genius II
