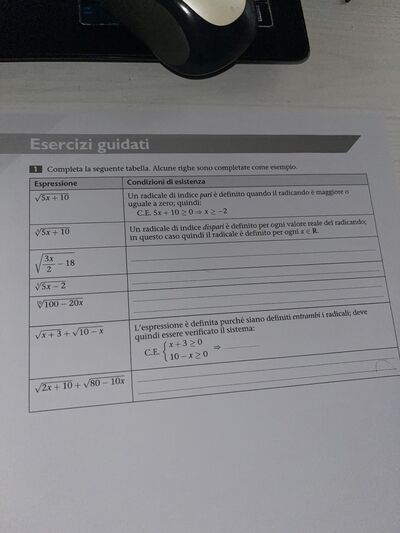
Completa la tabella
Condizioni di esistenza
- Un radicale di indice pari è definito quando il radicando è maggiore o uguale a zero; quindi:
C.E. $5 x+10 \geq 0 \Rightarrow x \geq-2$
- Un radicale di indice dispari è definito per ogni valore reale del radicando; in questo caso quindi il radicale è definito per ogni $x \in R$
- L'espressione è definita purché siano definiti entrambi i radicali; deve quindi essere verificato il sistema:
$$
\text { C.E. }\left\{\begin{array}{l}
x+3 \geq 0 \\
10-x \geq 0
\end{array} \Rightarrow\right.
$$