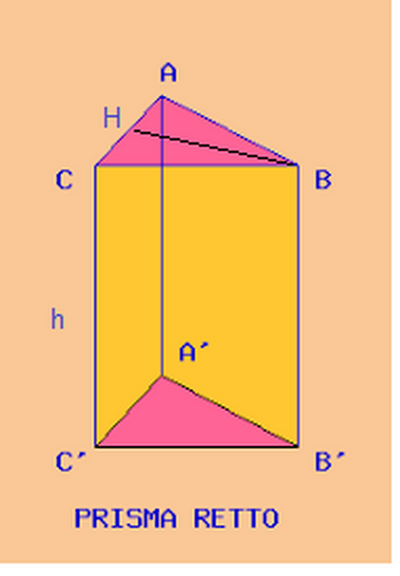
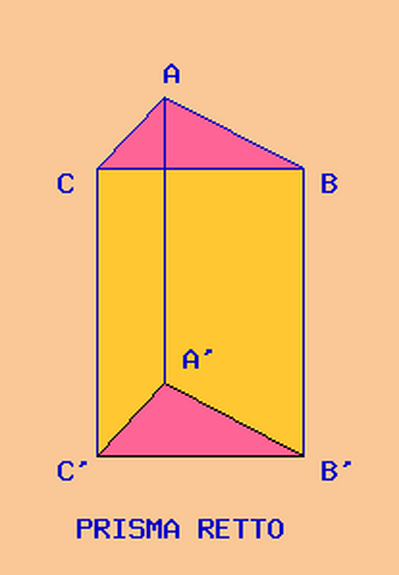
Primo problema
Un orisma retto la cui l'altezza musica 24 cm, ha per base un triangolo isoscele avente l'area di 27 cm2 .
Sapendo che la base del triangolo misura 12 cm, calcola l'area laterale del prisma.
Secondo porblema
La base di un prisma retto è un triangolo rettangolo avente di 150 cm2 e un cateto lungo 15 dm.
Calcola l'area laterale del prisma sapendo che la sua altezza è lunga 21dm.
Terzo problema
Un prisma retto alto 11 cm ha per base un triangolo rettangolo. Sapendo che i cateti del triangolo di base sono lunghi rispettivamente 40 cm e 42 cm, calcola l'area totale del prisma.
Quarto problema
La base di un prisma è un triangolo isoscele avente il perimetro di 81 cm e la base lunga 36 cm.
Calcola la misura dell'altezza del prisma sapendo che l'area della sua superficie totale è 1498,50cm2.
MI AIUTATE????