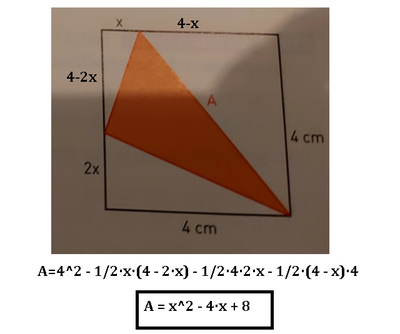
Per trovare l'area del triangolo colorato, troviamo l'area del quadrato e da essa togliamo le aree dei tre triangoli rettangoli bianchi attorno alla figura:
Area Quadrato = 4^2 = 16;
Area triangoli:
A1 = (4 - 2x) * x/2 = 2x - x^2 ; triangolo in alto a sinistra;
A2= (4 - x) * 4 / 2 = 8 - 2x; triangolo grande a destra;
A3 = 4 * 2x / 2 = 4x ; triangolo in basso;
A = 16 - (2x - x^2) - (8 - 2x) - 4x;
A = 16 - 2x + x^2 - 8 + 2x - 4x;
A = x^2 - 4x + 8;
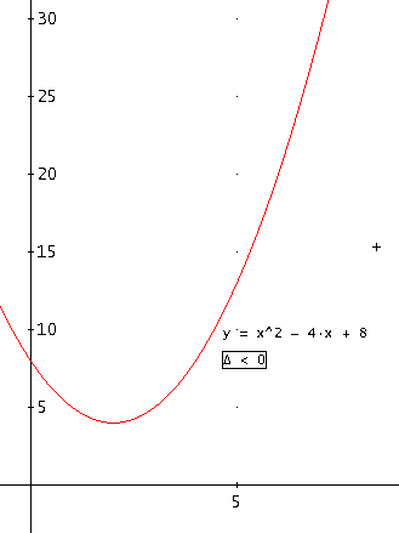
A è una parabola con vertice in (2; 4); per x = 0; y = +8;
per x = + 4; y = + 8.
Il grafico della parabola y = x^2 - 4x + 8 resta sopra l'asse delle x, y non ha valori negativi, l'area A è sempre positiva.
A = 5 cm^2;
x^2 - 4x + 8 = 5;
x^2 - 4x + 3 = 0;
x = 2 +- radice(4 - 3) = 2 +- 1;
x = 1; 1 - 4 + 8 = 5 cm^2 ;accettabile;
[x = 3; non accettabile perché il lato del quadrato è 4 cm; se x =3, il segmento 2x diventa 6;
2x supera 4 cm].
L'area A = x^2 - 4x + 8 non diventa mai 0;
x^2 - 4x + 8 = 0;
x = 2 +- radice(4 - 8);
radice(-4) non esiste fra i numeri reali, non si può fare.
Quindi A è sempre positiva.
Ciao @djj