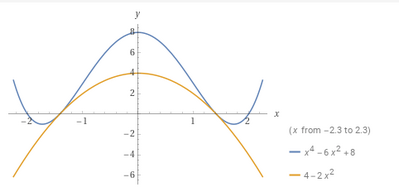
Considera la funzione di equazione $y=a x^4+b x^2+c$.
a. Determina i coefficienti $a, b$ e $c$ in modo che il suo grafico passi per il punto di coordinate $(1,3)$ e abbia un estremo relativo nel punto di coordinate $(\sqrt{3},-1)$.
b. Traccia il grafico della funzione in corrispondenza dei valori di $a, b$ e $c$ trovati.
c. Scrivi l'equazione della parabola con asse parallelo all'asse delle $y$ avente il vertice in $V(0,4)$, che sia tangente al grafico della funzione.
[a. $a=1, b=-6, c=8 ;$ b. $\max (0,8), \min (\pm \sqrt{3},-1)$; flessi: $( \pm 1,3) ;$ c. $\left.y=-2 x^2+4\right]$
ciao scusate, non riesco a trovare i parametri, allora io ho sostituito la X e y con i punti che danno è fatto la derivata ma mi manca una condizione per trovarli, e non riesco a capire come fare il punto (c)
grazie in anticipo