[Risolto] Matematica

@Richiuu

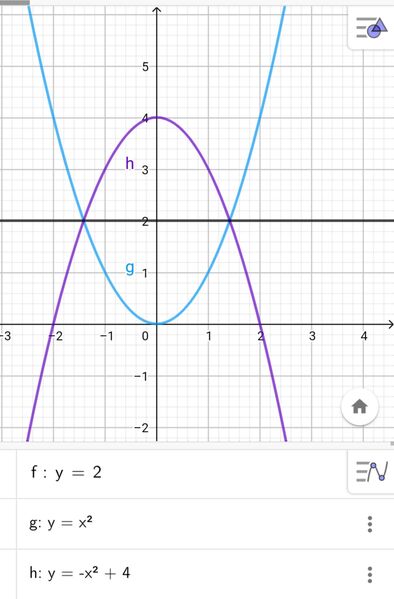
Simmetria rispetto ad una retta orizzontale: y=c

Si effettua la traslazione:

{X= x

{Y= 2*c - y

Con c=2

{X= x

{Y= 4 - y

Quindi la parabola simmetrica rispetto alla retta y=2 è:

4 - Y= X²

Y= - X² + 4

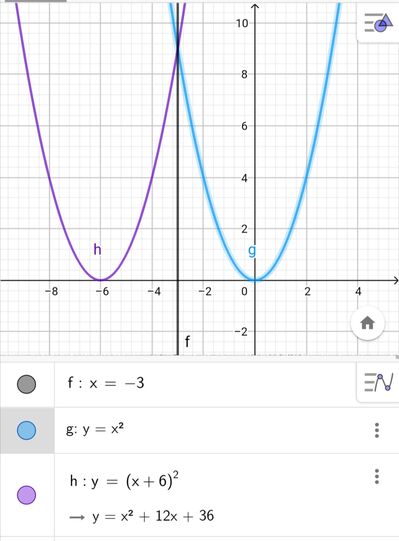
Simmetria rispetto ad una retta verticale: x=c

Si effettua la traslazione:

{Y= y

{X= 2*c - x

Con c= -3

{Y= y

{X= -6 - x

Quindi la parabola simmetrica rispetto alla retta x= - 3 è:

Y= (-6 - X)²

Y= (X+6)²

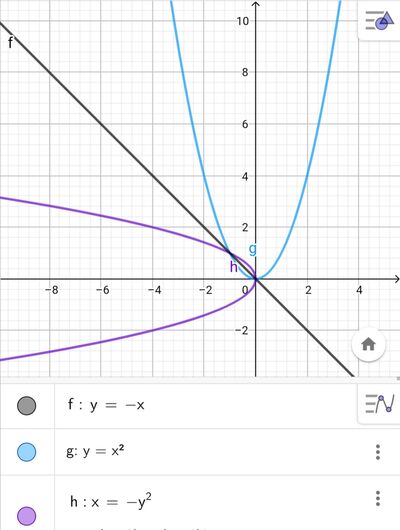
Simmetria rispetto alla bisettrice del secondo e quarto q. 

Si effettua la traslazione:

{X= - y

{Y= - x

Quindi la parabola simmetrica rispetto alla bisettrice è:

- X = Y²

X= - Y²

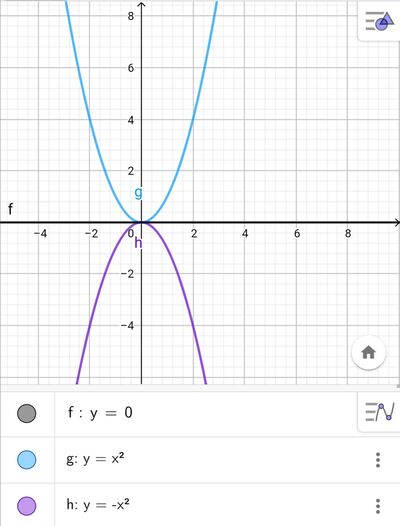
Simmetria rispetto all'asse x:

Si effettua la traslazione:

{X=x

{Y= -y

Quindi la parabola simmetrica rispetto rispetto asse x è:

- Y = X²

Y= - X²

Simmetria rispetto all'asse y:

{X= - x

{Y= y

Quindi la parabola simmetrica rispetto all'asse y è:

Y= X²