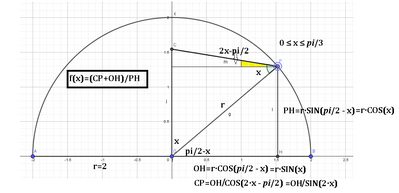
E’ data la semicirconferenza di diametro $\overline{A B}=4$ e centro $O$. Sul raggio perpendicolare ad $A B$ considera un punto $C$ tale che $C P \cong C O$, con $P$ punto appartenente alla semicirconferenza. Indica con $H$ la proiezione di $P \operatorname{su} A B$
a. Esprimi la funzione $f(x)=\frac{\overline{C P}+\overline{O H}}{\overline{P H}}$, con $x=C \widehat{P O}$.
b. Determina le limitazioni per $x$ e trova per quali valori di $x$ si ha $f(x)>1$.
$\left[\right.$ a) $f(x)=\frac{1+\sin 2 x}{1+\cos 2 x} ;$ b) $\left.0 \leq x \leq \frac{\pi}{3}, \frac{\pi}{8}<x \leq \frac{\pi}{3}\right]$