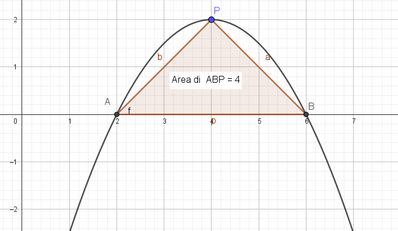
Scrivi l'equazione della parabola avente il vertice nel punto $P(4 ; 2)$ e il fuoco di coordinate $\left(4 ; \frac{3}{2}\right)$. Calcola poi l'area del triangolo che ha come vertici il vertice della parabola e le sue intersezioni con l'asse delle ascisse.
$$
\left[y=-\frac{1}{2} x^2+4 x-6 ; 4\right]
$$
Ciao se potete mi aiutate per favore? grazie
187
punti
Livello 1
y = a·x^2 + b·x + c
[4, 2] coordinate del vertice
[4, 3/2] coordinate del fuoco
a < 0 perché il fuoco sta sotto il vertice
Quindi:
{1/(4·a) = 3/2 - 2
{2 = a·4^2 + b·4 + c (passa per il vertice)
{- b/(2·a) = 4 (equazione asse)
quindi:
{a = - 1/2
{16·a + 4·b + c = 2
{b/a = -8
Risolvo ed ottengo: [a = - 1/2 ∧ b = 4 ∧ c = -6]
Equazione parabola: y = - x^2/2 + 4·x - 6
{y = - x^2/2 + 4·x - 6
{y = 0
Risolvo ed ottengo le intersezioni richieste:
[x = 2 ∧ y = 0, x = 6 ∧ y = 0]
Quindi area triangolo di vertici:
[2, 0]
[6, 0]
[4, 2]
Α = 1/2·ABS(2 - 6)·2----> Α = 4
94075
punti
Genius II
@lucianop grazie mille, buon pomeriggio
Di nulla. Buon pomeriggio pure a te.
I prescritti punti di vertice V(4, 2) e di fuoco F(4, 3/2) sono allineati sulla x = 4 che quindi è l'asse di simmetria, parallelo all'asse y; pertanto l'equazione della parabola Γ richiesta ha la forma
* Γ ≡ y = 2 + a*(x - 4)^2
dove l'apertura a si determina dalla relazione
* yF = yV + 1/(4*a) ≡
≡ 3/2 = 2 + 1/(4*a) ≡ a = - 1/2
da cui
* Γ ≡ y = 2 - (x - 4)^2/2 ≡
≡ y = - x^2/2 + 4*x - 6 ≡
≡ y = - (1/2)*(x - 2)*(x - 6)
-----------------------------
I due zeri X(4 ± 2, 0), cioè X1(2, 0) oppure X2(6, 0), distano due dall'asse il che è quanto V dista dal loro segmento; quindi l'area S del triangolo VX1X2 è
* S = (xX2 - xX1)*yV/2 = (6 - 2)*2/2 = 4
57363
punti
Genius I
@exprof grazie buon pomeriggio
