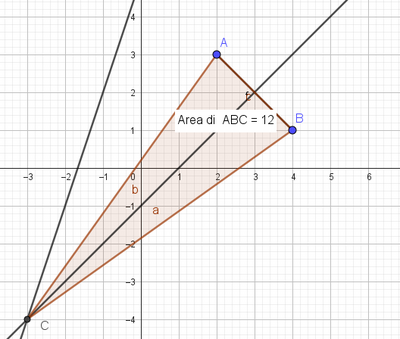
Dati due punti $A(2 ; 3), B(4 ; 1)$ e la rettar $r$ di equazione $3 x-y+5=0$, determina su $r$ un punto $C$ in modo che il triangolo $A B C$ sia isoscele sulha brse $A B$ e calcola Parea del triangolo $A B C$.
$$
\{C(-3 ;-4) ; 12\}
$$
Non capisco per favore
256
punti
Livello 1
Asse del segmento AB
[x, y] punto sull'asse del segmento AB
[2, 3] A
[4, 1] B
(2 - x)^2 + (3 - y)^2 = (4 - x)^2 + (1 - y)^2
x^2 - 4·x + y^2 - 6·y + 13 = x^2 - 8·x + y^2 - 2·y + 17
risolvo rispetto ad y: y = x - 1
Determino C
{y = 3·x + 5
{y = x - 1
risolvo: [x = -3 ∧ y = -4]
Area
[2, 3]
[4, 1]
[-3, -4]
[2, 3]
Α = 1/2·ABS((2·1 + 4·(-4) + (- 3)·3) - (2·(-4) +(- 3)·1 + 4·3))
Α = 1/2·ABS(-23 - 1)-----> Α = 12
94792
punti
Genius II
